FE501 – 1005
Syllabus
Topics:
For each in x where x belongs to:
- Linear Programming (LP)
- Integer Linear Programming (ILP)
- Nonlinear Programming (NLP)
- Dynamic Programming (DP)
For each of the x:
- formulation of
xmodels - solution of
xmodels - applications in finance and economics
Outline (week by week)
Introduction
LP
- Formulation
- Graphical Solution Procedure
- Simplex Method
- Exel-Solver
- GAMS Optimization Package
LP: Applications to Finance and Economics
Duality and Sensitivity
ILP
- Formulation
- Branch-and Bound method
ILP: Applications to Finance and Economics
Nonlinear Optimization
- Formulation
- Unconstrained and constrained NLP models
- Solution methods
- KKT conditions
Continue 7
Quadratic Programming and Portfolio Optimization
Thechniques for Calculating the Efficient Frontier
DP
- Formulation
- Solution
DP: Applications to Finance and Economics
Summary
Introduction
Typiclly optimization problems have the goal of allocating limited resources to alternative activitites in order to maximize the total benifit obtained from those activities.
Optimization is now being used as an effective management and decision-support tool.
Classes of optimization problems:
- Linear
- Quadratic
- Integer
- Dynamic
- Stochastic
- Conic
- Nonlinear
What is optimization?
Optimization is the process of finding the best way of making decisions that satisfy a set of constraints.
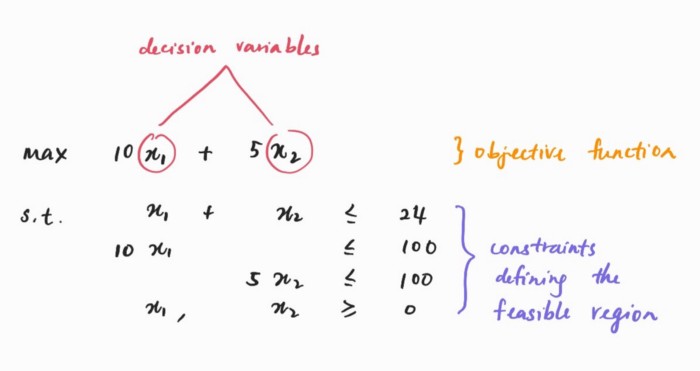
What is linear programming?
Linear Programming (LP) is also called linear optimization.
- minimize or maximize a linear objective
- subject to linear equalities and inequalities
Example:
A feasible solution satisfies all of the constraints. x = 1, y = 1 is feasible [1] ; x = 1, y = 3 is infeasible.
An optimal solution is the best feasible solution. The optimal solution for above problem is


What is decision variables? objective functions ?constraints ?
Example Problem Soling
Turing machine and NP-Hard (just hard…)

Knapsack Probelm

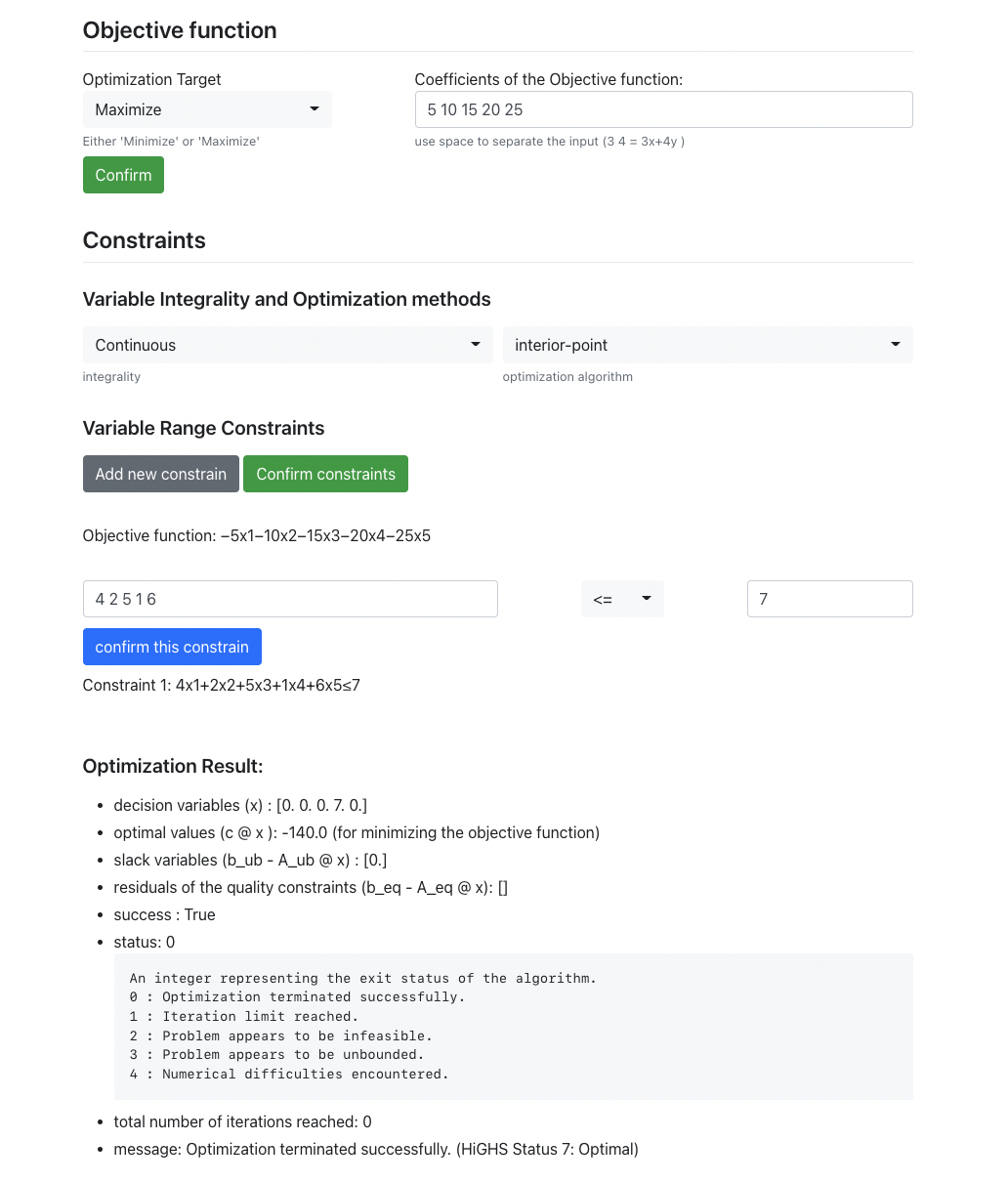
Q: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.
| Items | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Weight (Kg) | 4 | 2 | 5 | 1 | 6 |
| Utility | 5 | 10 | 15 | 20 | 25 |
| Capacity | 7 Kg |
|---|
Target: Maximize the Total Utility
Possible solutions are called
feasible solutions
To solve such a problem If the number of possible solutions are small then we can use:
- Brute-forch approach
- Complete enumeration
- Exhaustive enumeration
Problem Definition:
The model above (3) called integer linear model.
Generally A standard linear program will be:
Using Excel

Using Optimator
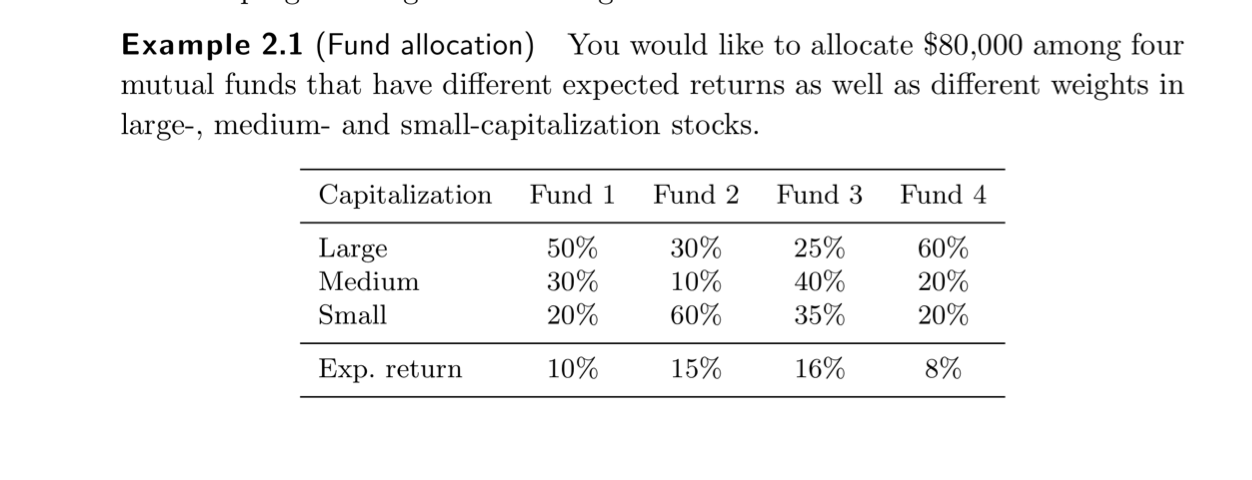
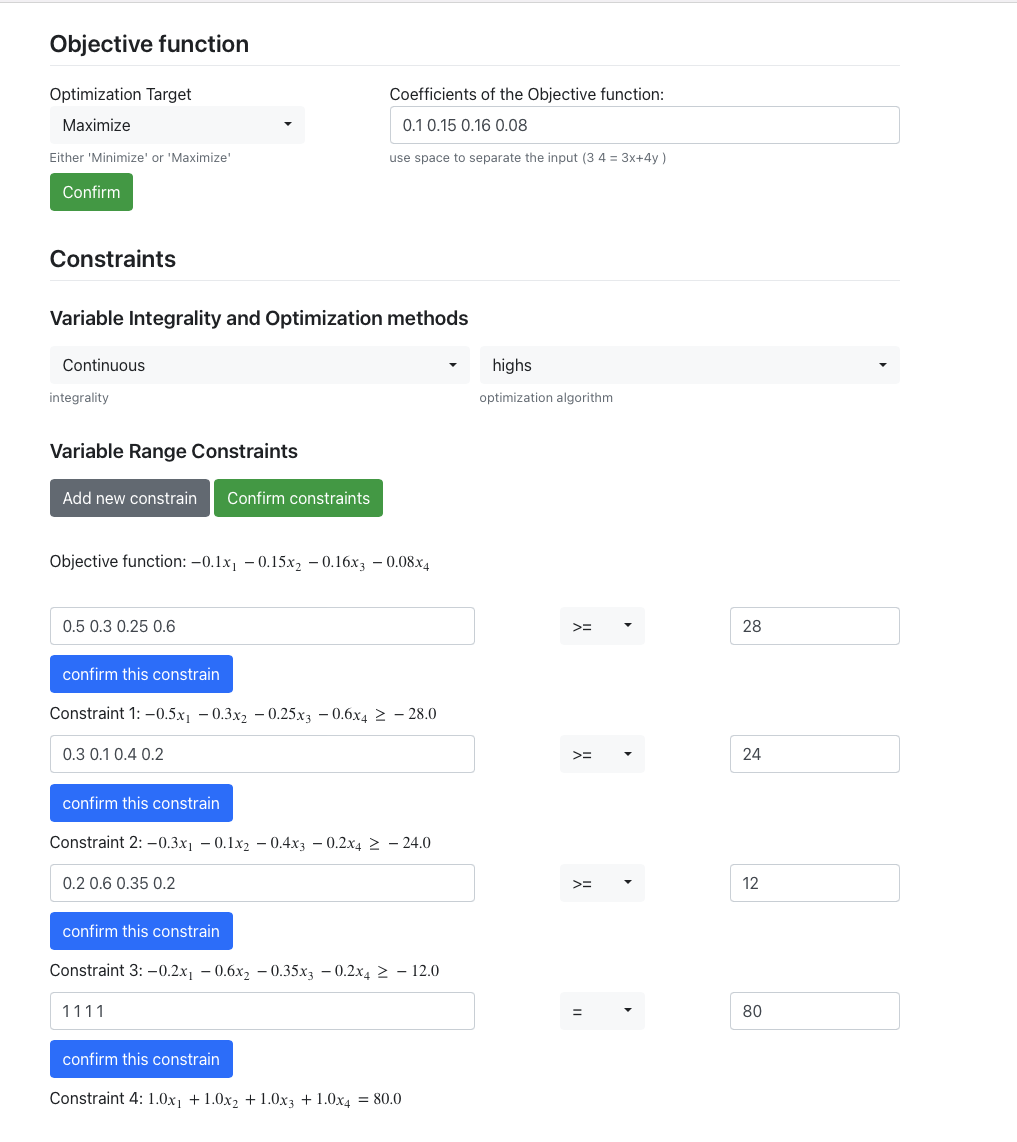
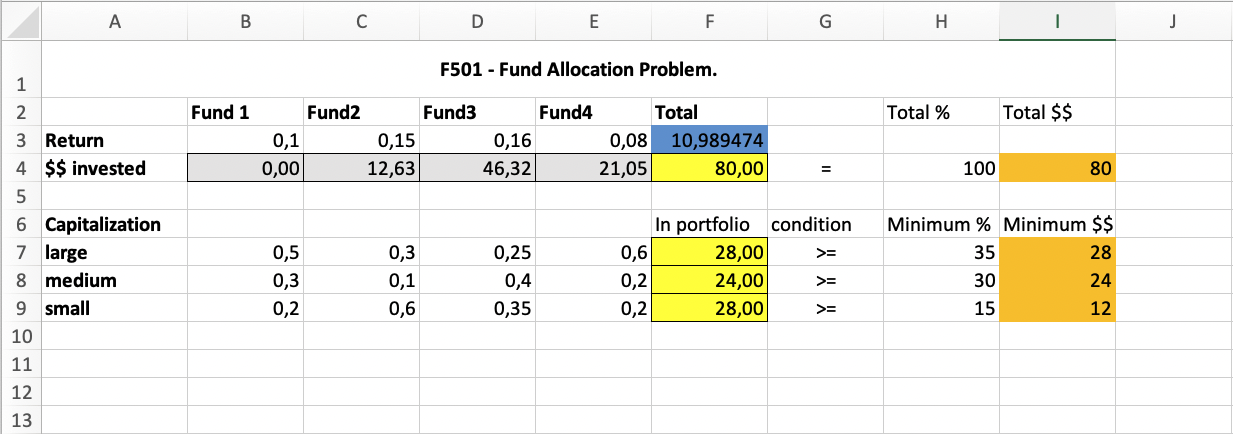
Fund allocation problem

Using optimator
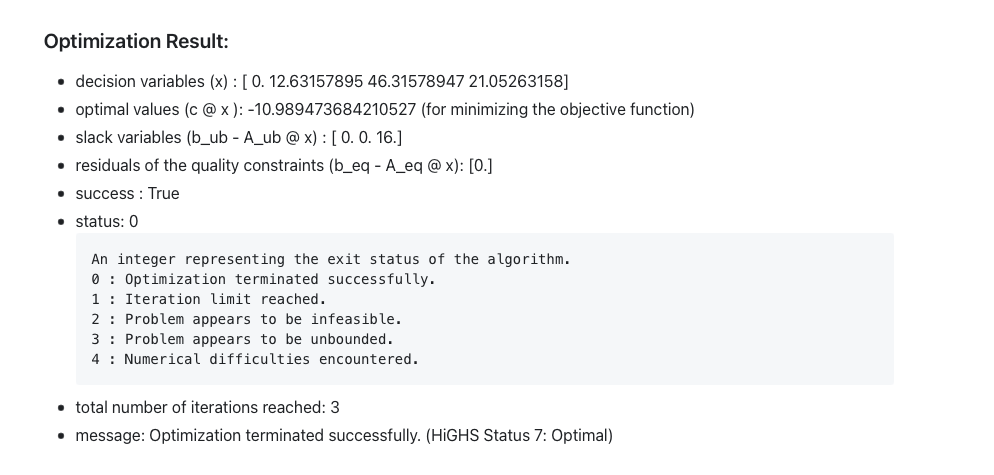
Using Excel
Possible results from Excel Solver can be:
- Find the solution
- Multiple Optimal
- Optimal
- No feasible solution.
Graphical method
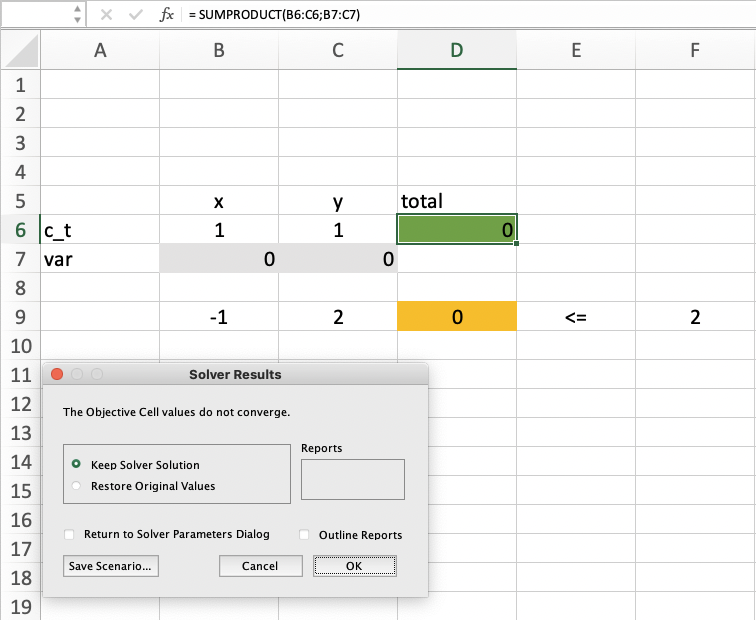
"The Objective Cell values do not converge" means there is no limit to the objective function value.
1import matplotlib.pyplot as plt2import numpy as np3x = np.linspace(-15,50)4y1 = 2+x5fig = plt.figure(dpi=300)6ax = fig.add_subplot(111)7ax.grid(True, which='both')8ax.axhline(y=0, color='k')9ax.axvline(x=0, color='k')10ax.plot(x,y1,label='y=x+2') # y = x+211ax.plot(np.zeros(50),x,label='x=0') # x = 012ax.plot(x,np.zeros(50),label='y=0') # y = 013ax.plot(x,-x,label='y=-x+z (z=0)')14ax.plot(x,-x+10,label='y=-x+z (z=10)')15ax.plot(x,-x+20,label='y=-x+z (z=20)')16plt.legend()17plt.show()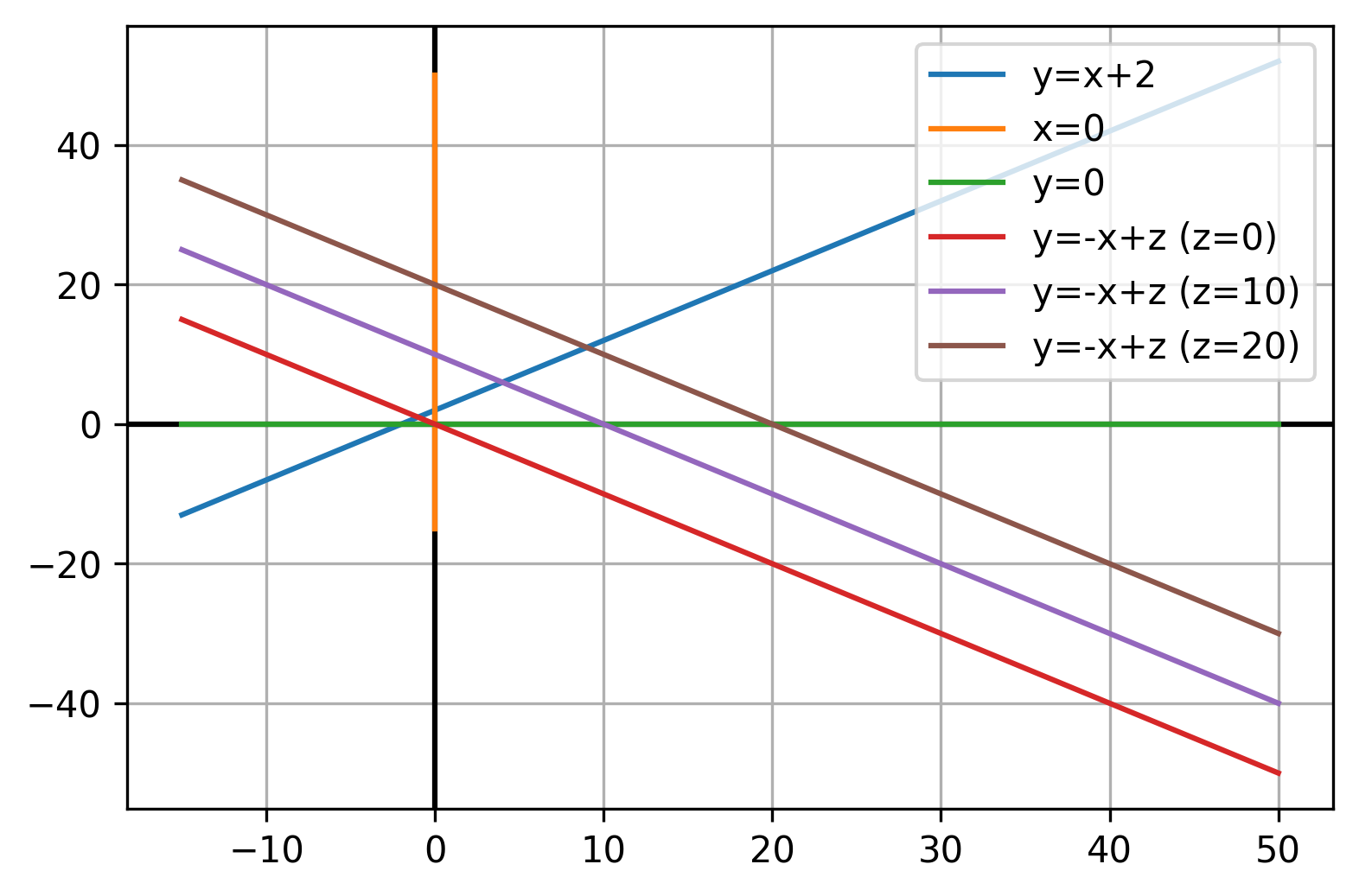
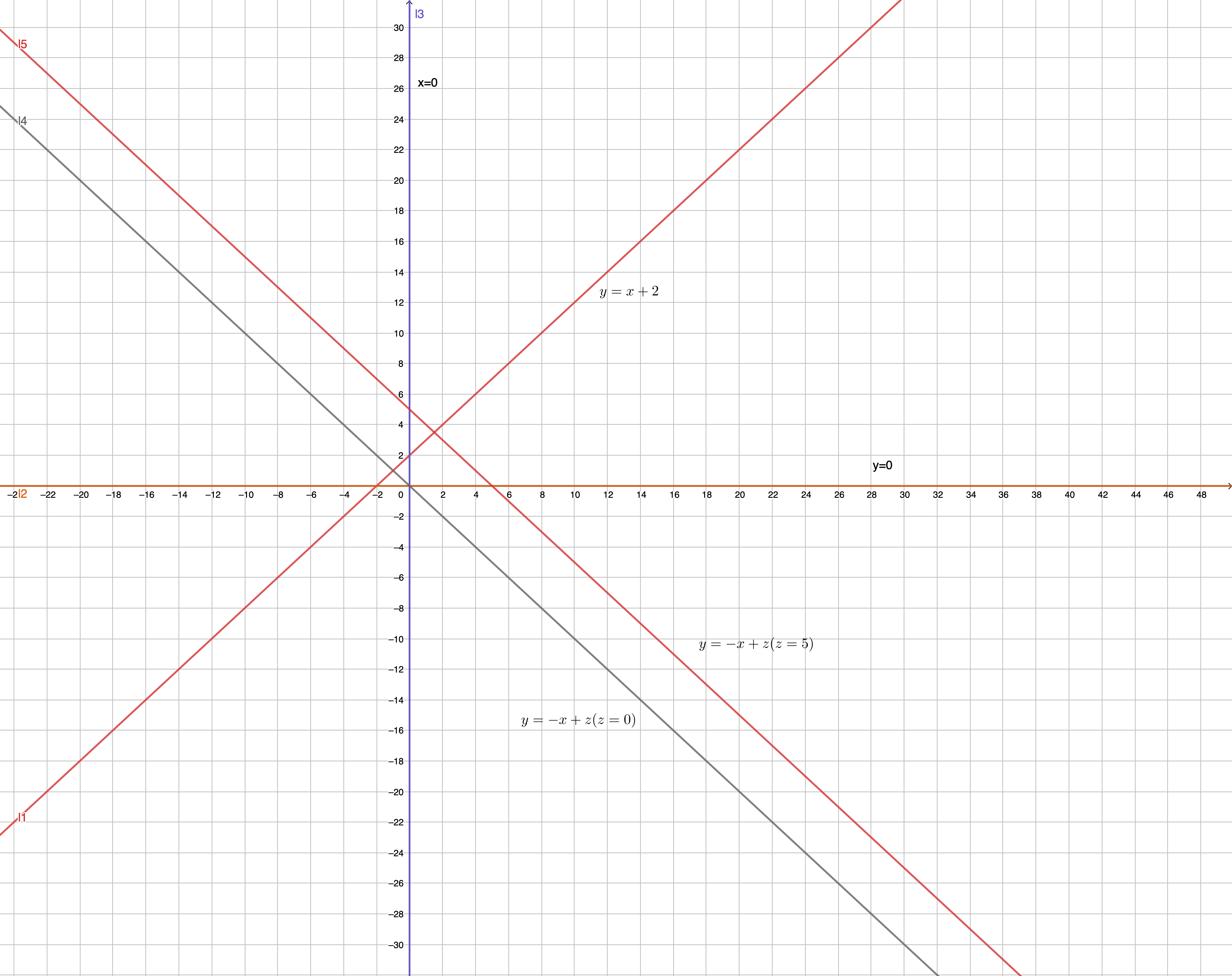
Result: to maximize
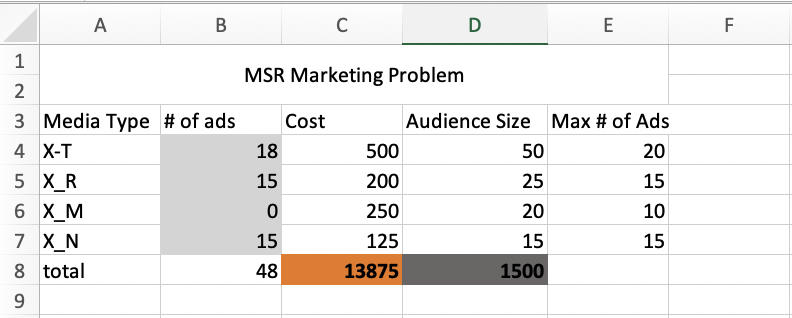
MSR Marketing example

Decision variables :
Objective function
*Minimize
Constraints
Scipy for Calculating the LineProg
x1ask = input("Enter coefficients of the linear objective function (separate with space), enter 'q' to stop.")2
3objective_function_coefficients_str = ask.strip().split(" ")4objective_function_coefficients = [float(x) for x in objective_function_coefficients_str]5print(f"Objective Function Coefficients: {objective_function_coefficients}")6
7while True:8 optimization_type = input("Select Optimization Type: 1.Minimize, 2.Maximize ")9 if optimization_type in ['1', '2']:10 break11
12if optimization_type == '2':13 # This is a maximization problem and we need to invert it14 objective_function_coefficients = [-1 * x for x in objective_function_coefficients]15
16constraints_lhs_ineq = []17constraints_rhs_ineq = []18
19constraints_lhs_eq = []20constraints_rhs_eq = []21
22while True:23
24 lhs = input("Input constraints left hand side coefficients.")25 operator = input("Input operator for the equation.('le','ge','eq')")26 rhs = input("Input constraints right hand side coefficient.")27
28 lhs_str = lhs.strip().split(" ")29 lhs = [float(x) for x in lhs_str]30
31 rhs_str = rhs.strip()32 rhs = float(rhs_str)33
34 if operator == 'le':35 constraints_lhs_ineq.append(lhs)36 constraints_rhs_ineq.append(rhs)37 elif operator == 'ge':38 lhs = [-1 * x for x in lhs]39 rhs = -1 * rhs40 constraints_lhs_ineq.append(lhs)41 constraints_rhs_ineq.append(rhs)42 elif operator == 'eq':43 constraints_lhs_eq.append(lhs)44 constraints_rhs_eq.append(rhs)45
46 ask = input("Continue for other constraints? Y/N (Y)")47
48 if ask in ['N', 'n', 'q']:49 break50
51print("objective_function_coefficients", objective_function_coefficients)52print("constraints_lhs_ineq", constraints_lhs_ineq)53print("constraints_rhs_ineq", constraints_rhs_ineq)54print("constraints_lhs_eq", constraints_lhs_eq)55print("constraints_rhs_eq", constraints_rhs_eq)56
57for each in [constraints_lhs_eq, constraints_rhs_eq]:58 if each == []:59 each = None60 61opt = linprog(c=objective_function_coefficients, A_ub=constraints_lhs_ineq, b_ub=constraints_rhs_ineq, A_eq=constraints_lhs_eq, b_eq=constraints_rhs_eq)62print(opt)
Extra