FE501 – 1019

FE501 – 1019Graphical solution with Isoprofit linesChanging the slope of the Linear functionSimplex Algo StepsMake it to standard form First Hypothesis (x1=0,x2=0)Second Hypothesis (1,0,0,4)(Matrix) Transformation in the linear system of equationsSolving linear systems with matricesSolving the original problem with matrix notationShort - term finance ProblemExtra - Answers to the Book Excersises Exercise 2.1Exercise 2.2Exercise 2.3 **Exercise 2.4Example:Exercise 2.5 **

Graphical solution with Isoprofit lines

\begin{matrix} max 20 x_{1} + 10 x_{2} \\ s.t. x_{1} - x_{2} \leq 1 \\ 3 x_{1} + x_{2} \leq 7 \\ x_{1}, x_{2} \geq 0 \end{matrix}

Steps

Draw constraint boundary lines
Get intersections and feasible region
Draw parallel isoprofit lines

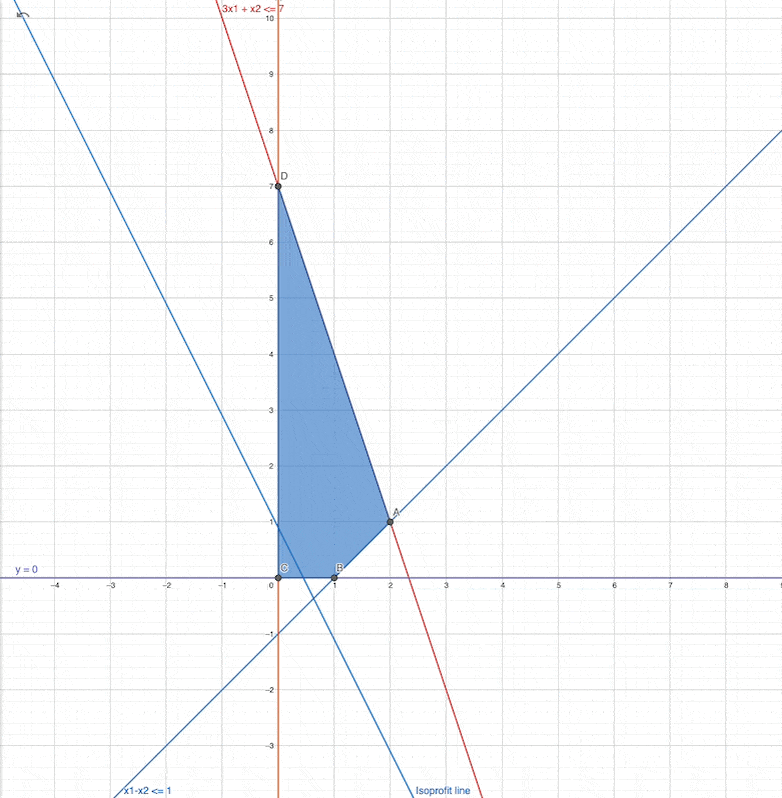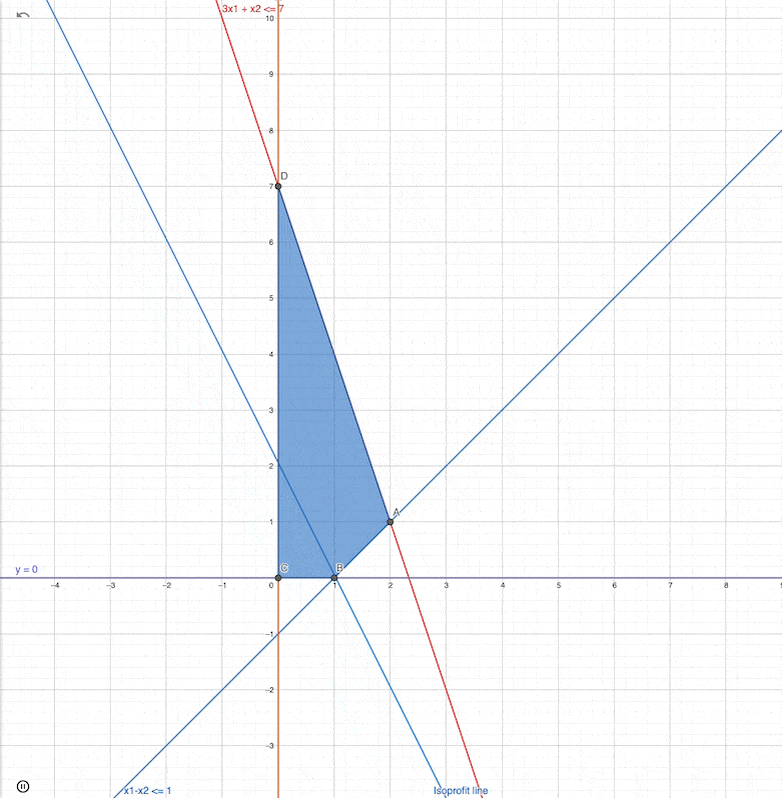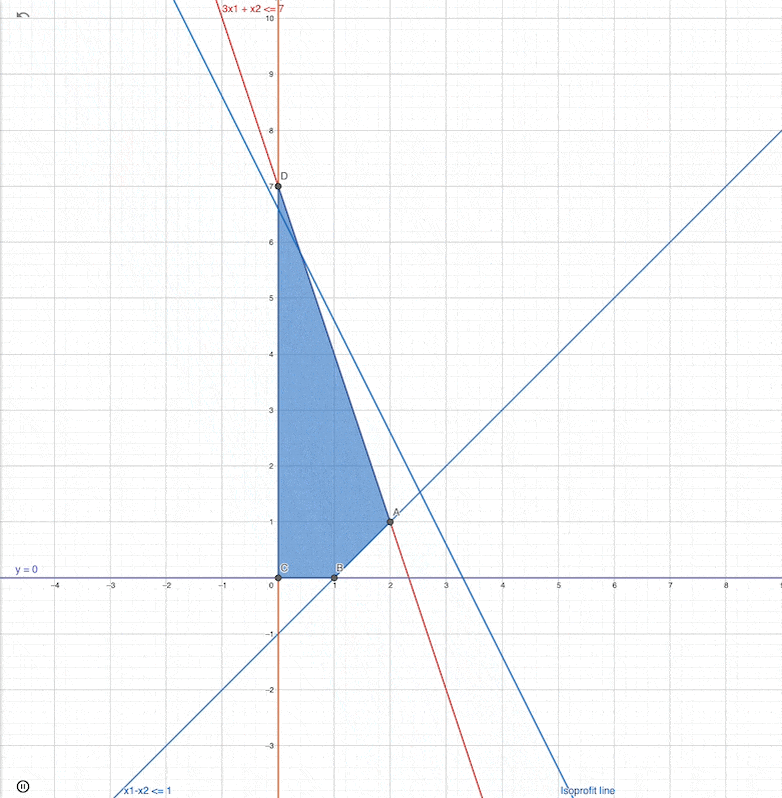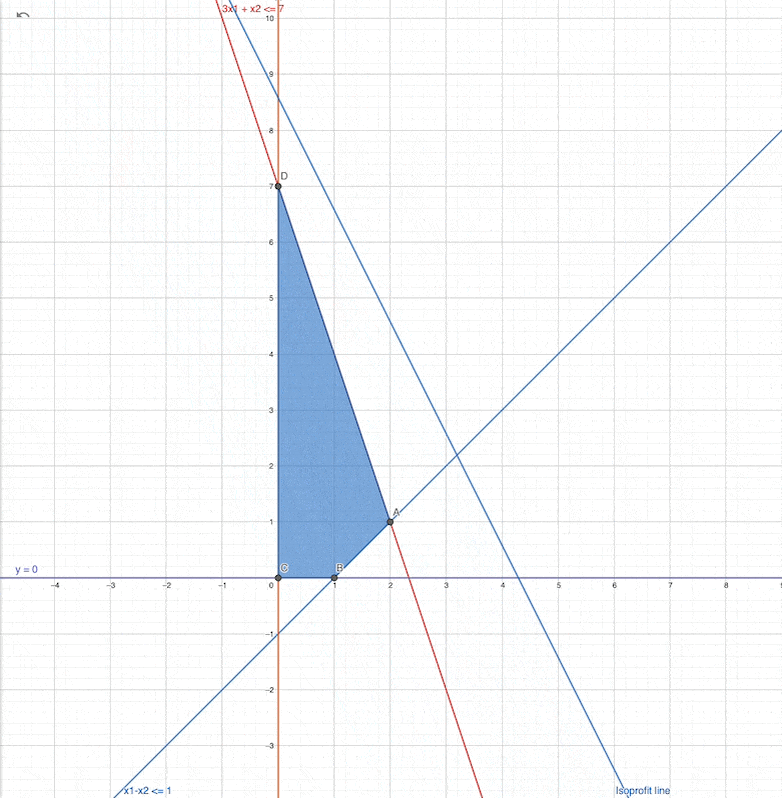
CleanShot 2022-10-27 at 13.35.33

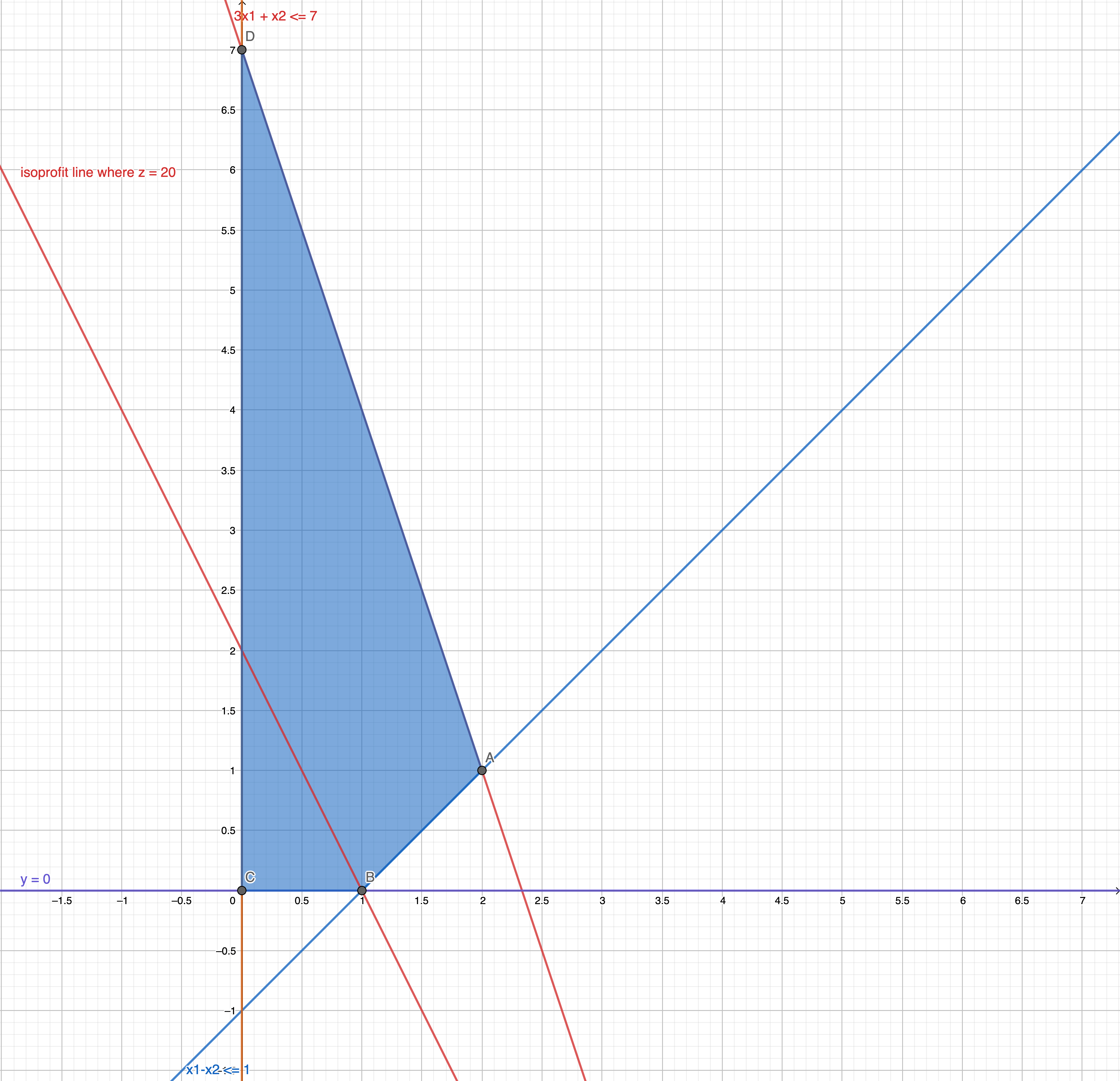
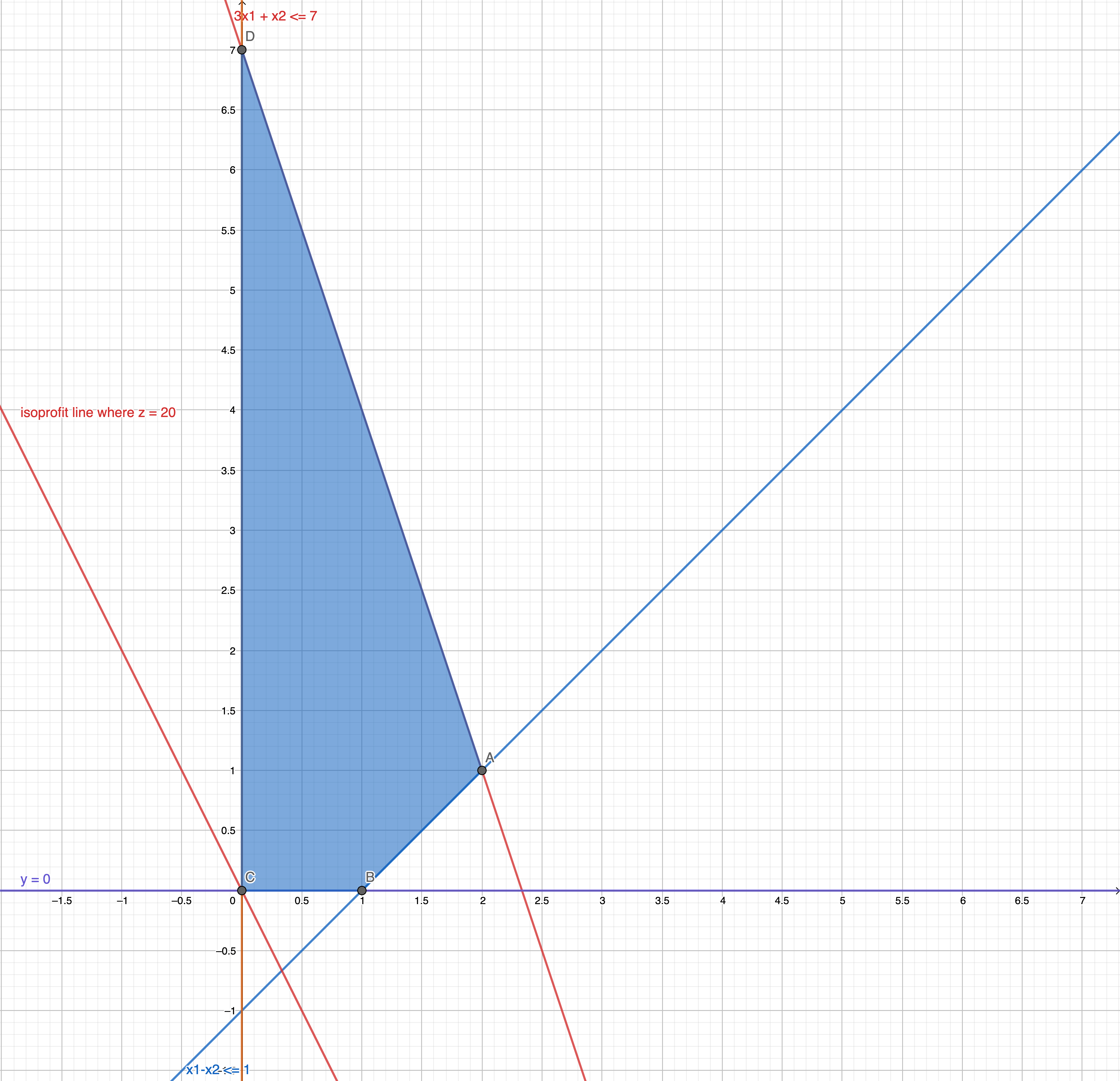
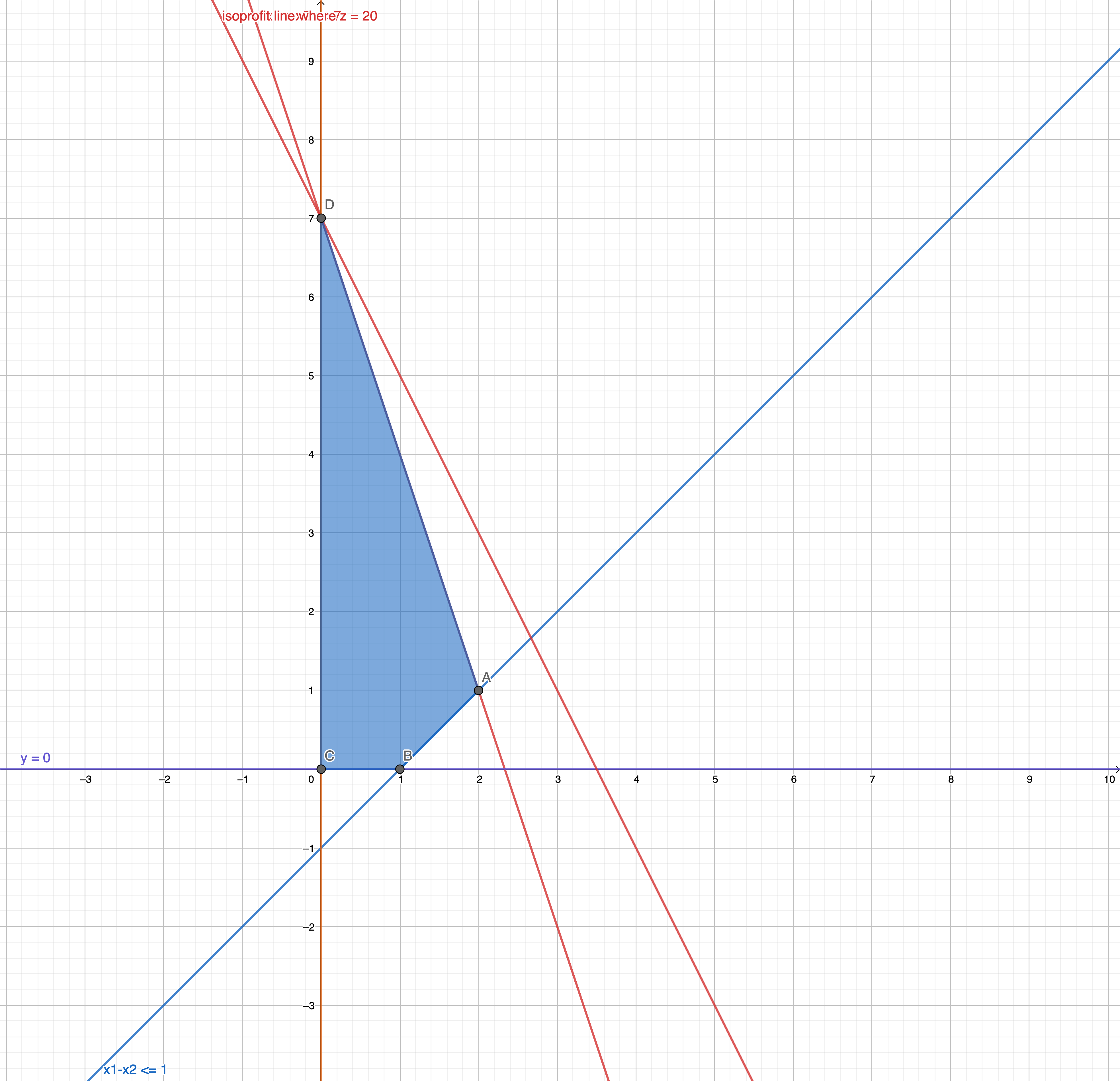
Changing the slope of the Linear function

What happens if we change the objective function as:

\begin{matrix} max 20 x_{1} + 10 x_{2} \Rightarrow 15 x_{1} + 10 x_{2} \\ s.t. x_{1} - x_{2} \leq 1 \\ 3 x_{1} + x_{2} \leq 7 \\ x_{1}, x_{2} \geq 0 \end{matrix}

slope of the original problem

\begin{matrix} 20 x_{1} + 10 x_{2} = z \\ 10 x_{2} = - 20 x_{1} + z \\ ∴ s_{1} = - 2 \end{matrix}

slope of the changed problem (similarly):

s_{2} = - \frac{15}{10} = - 1.5

\begin{matrix} c_{1} x_{1} + c_{2} x_{2} = z \\ slope = - \frac{c_{1}}{c_{2}} \end{matrix}

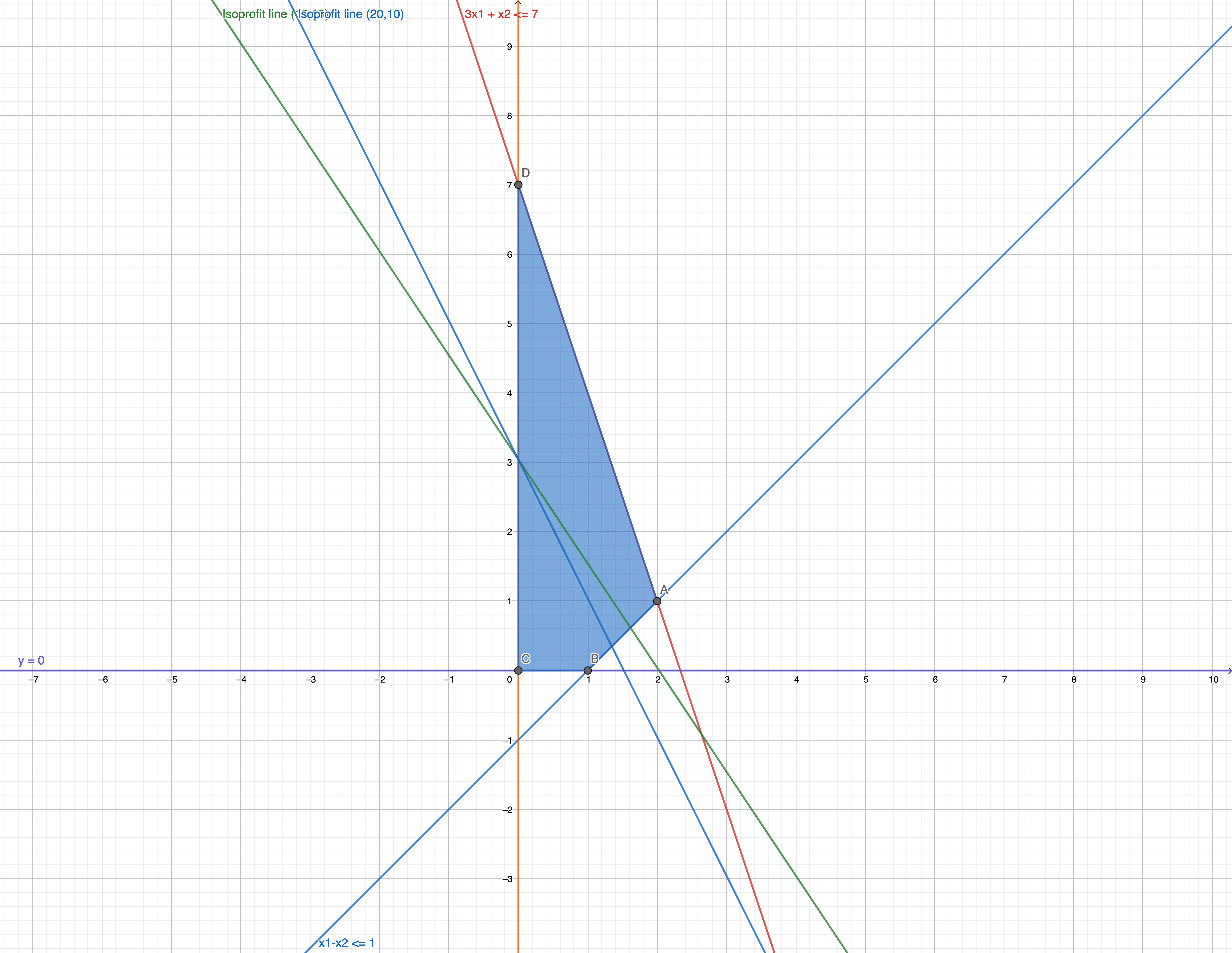
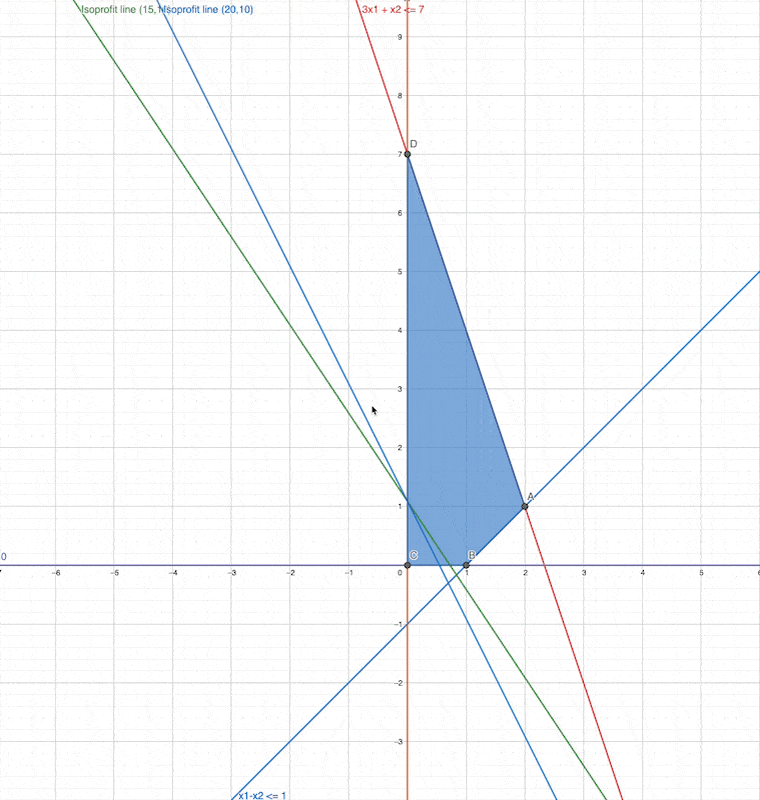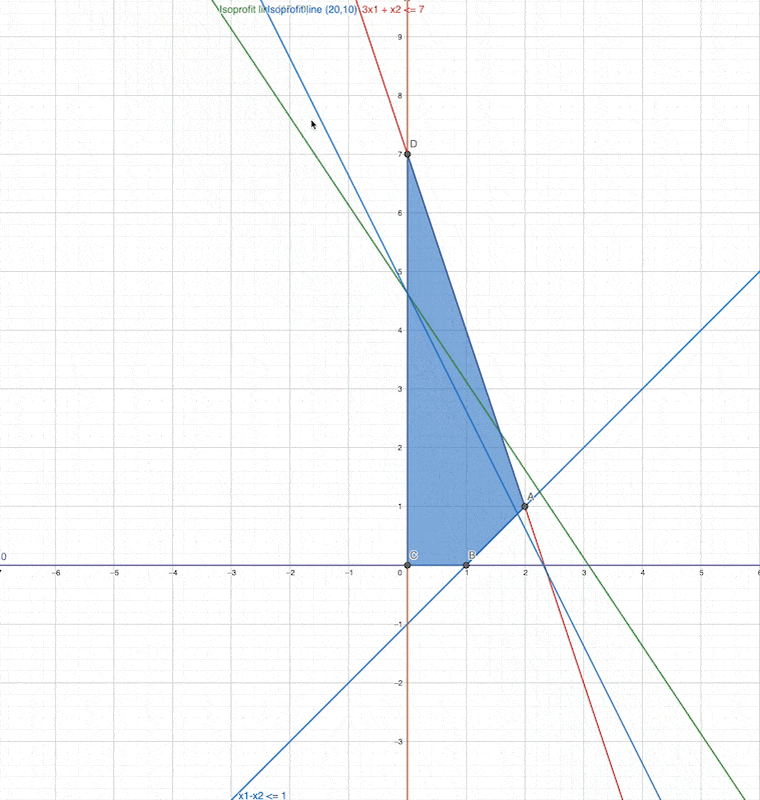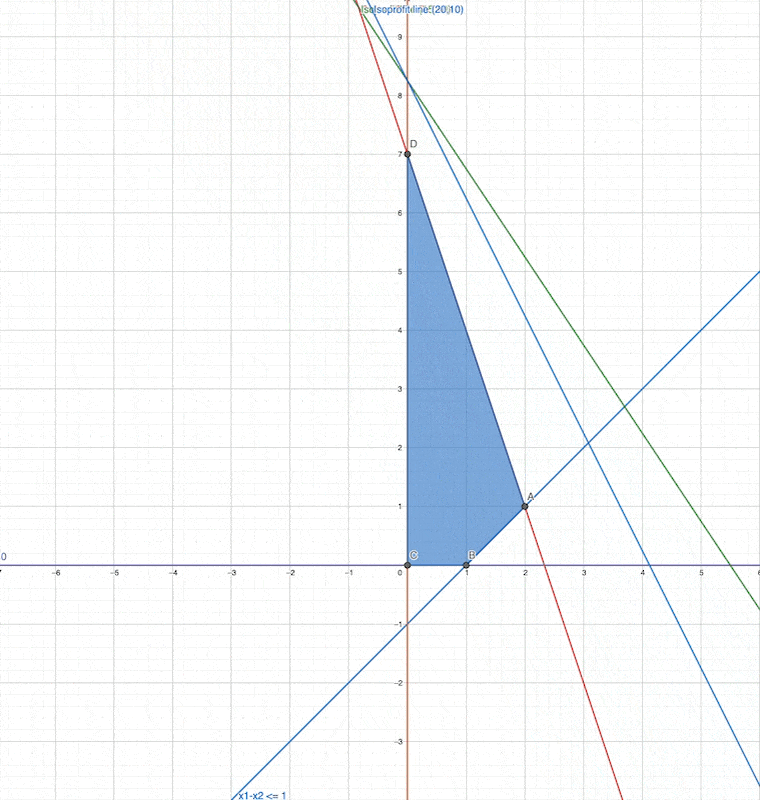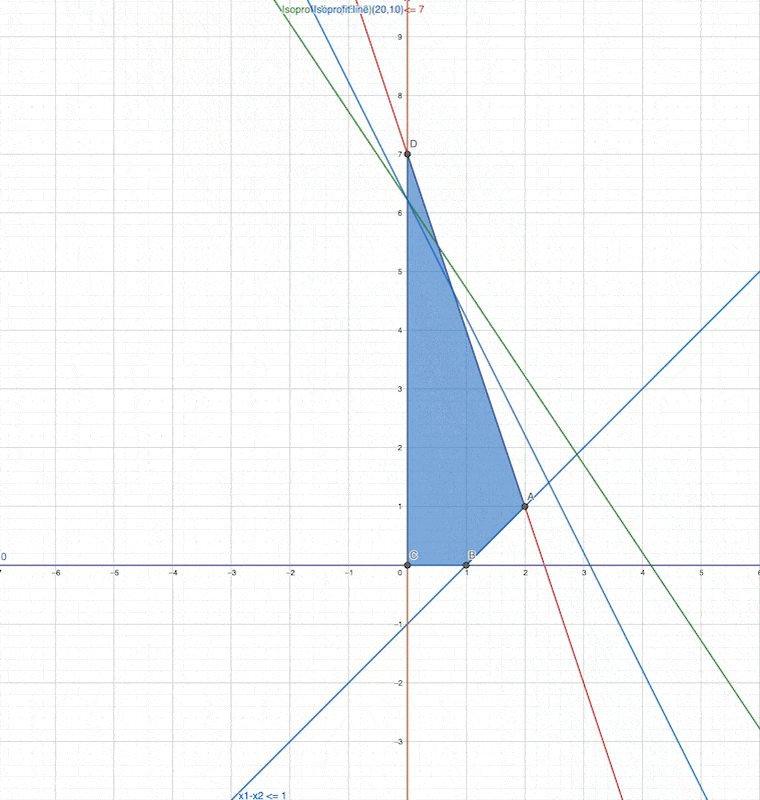
CleanShot 2022-10-27 at 13.57.23

We changed the slope, but the optimav value and the optimal solution (optimal point ) did not changed

In other words,

In the original problem, to get the maximum value

\begin{matrix} 20 x_{1} + 10 x_{2} = 70 \\ x_{2} = \frac{70 - 20 x_{1}}{10} \end{matrix}

In other words,

- \frac{c 1}{c 2}

is always the slope of the isoprofit line which are the slope of the objective functions of the linear programming.

Which corner point will be the optimal solution when the slope changed to the second one?

same

what happens if slope = -4 ?

What happens if slope = 1 ?

z = 10 x_{1} - 10 x_{2}

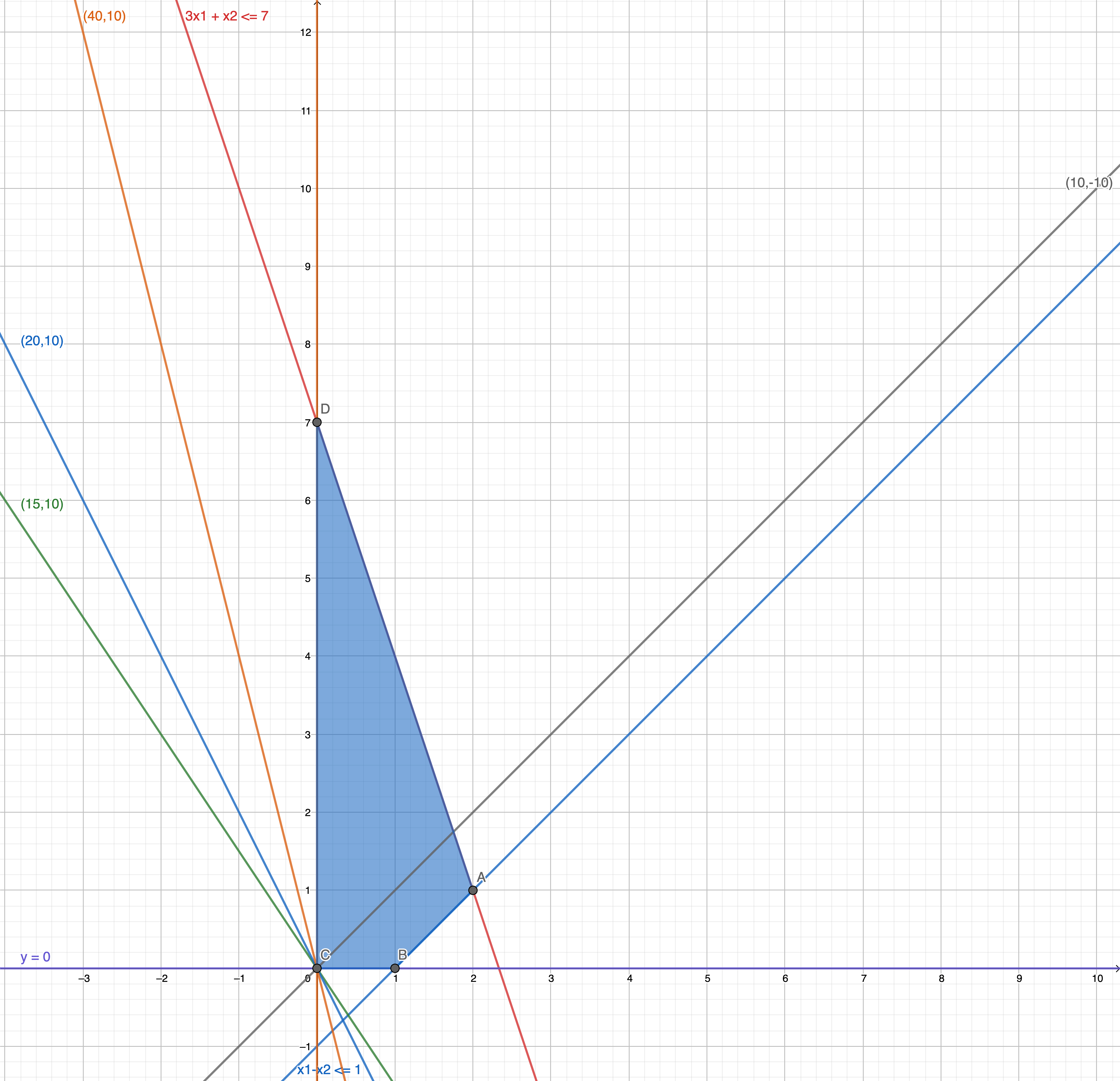
which is the optimal solution for this then?

m a x : z = 10 x_{1} - 10 x_{2}

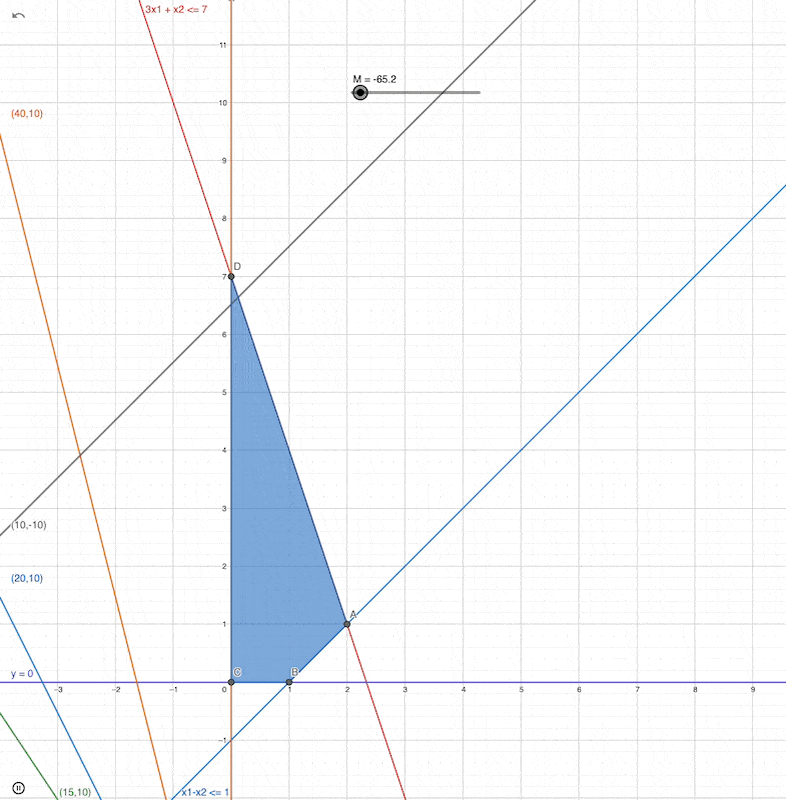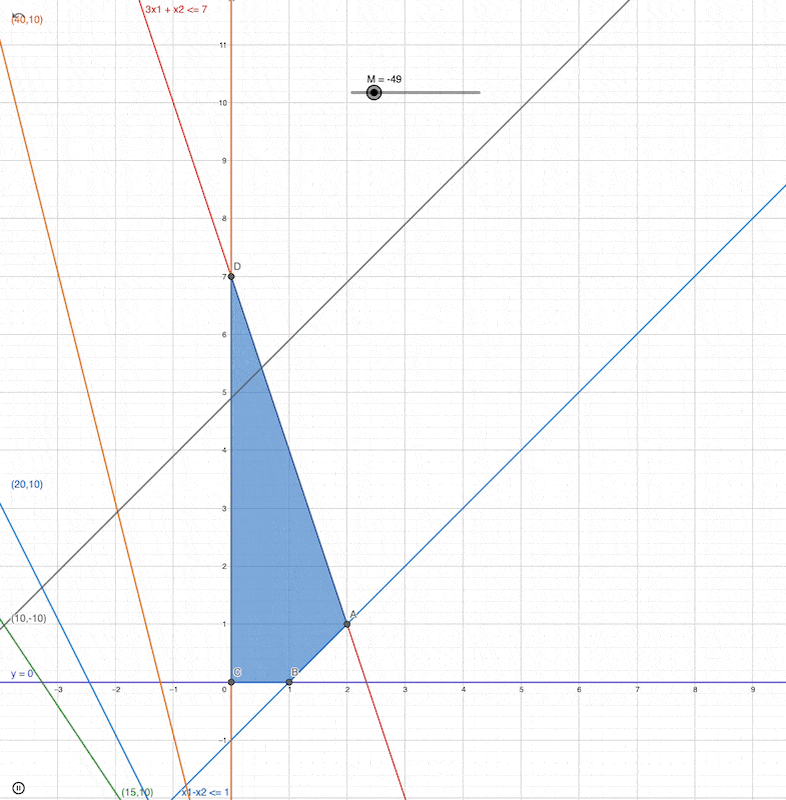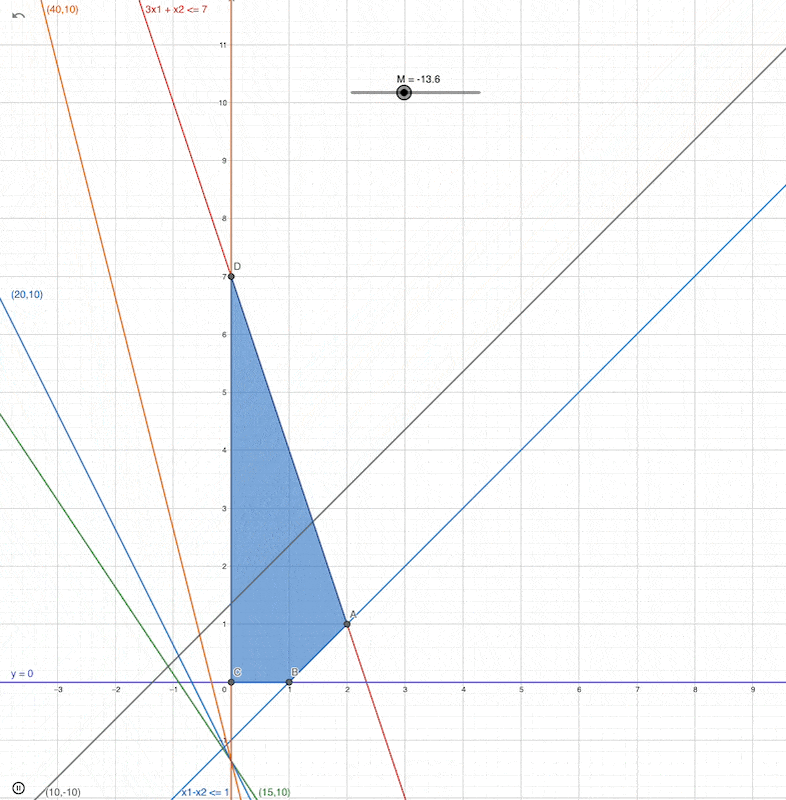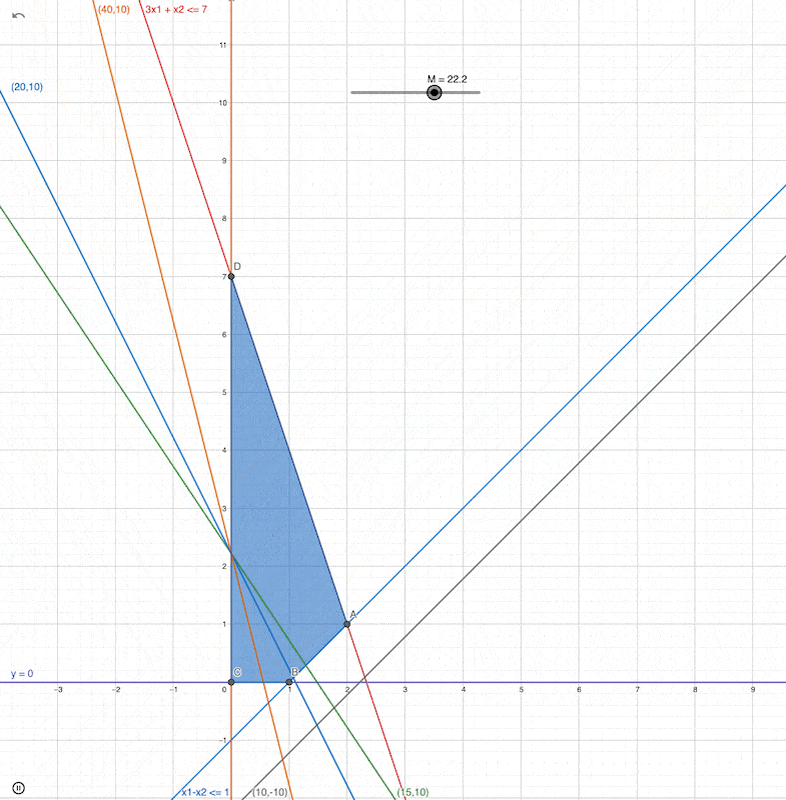
CleanShot 2022-10-27 at 14.09.33

Simplex Algo Steps

Make it to standard form

\begin{matrix} min (max) Z = c^{T} x \\ s.t. A x = b \\ x, b \geq 0 \end{matrix}

In this case, we have

\begin{array}{r} max 20 x_{1} + 10 x_{2} \\ s.t. x_{1} - x_{2} \leq 1 \\ 3 x_{1} + x_{2} \leq 7 \\ x_{1}, x_{2} \geq 0 \end{array}

and we have two inequality functions, so we will introduce two slack variables:

\begin{array}{r} max z = 20 x_{1} + 10 x_{2} + 0 x_{3} + 0 x_{4} \\ s.t. x_{1} - x_{2} + x_{3} = 1 \\ 3 x_{1} + x_{2} + x_{4} = 7 \\ x_{i} \geq 0, i = 1, 2, 3, 4 \end{array}

We can not solve if we have two equations and 4 unknowns.

A system of linear equations, can be solved if you have n equations and n unknowns or variables.

So, this can be solved:

\begin{matrix} x + y = 2 \\ 2 x - y = 5 \end{matrix}

but we can not solve this:

\begin{matrix} x + y + z = 2 \\ 2 x - y - z = 5 \end{matrix}

To solve this, we need to assume and give z some value, for example :

\begin{matrix} l e t z = 0 \\ x + y = 2 \\ 2 x - y = 5 \end{matrix}

so we converted the problem to a solveable problem,

x = 7 / 3, y = - 1 / 3

In general, we have n decision variables and m equations. most of the time we have:

n \geq m

what we do in simplex method is, in each iteration we make

\begin{matrix} n - m variables = 0 \\ and solve remaining equations \end{matrix}

So we have:

Set n-m variables to zero.
solve m equations in m variables

Non-basic variables: their value if equal to zero.

Basic variables: their value is non-zero

for our problem,

\begin{array}{r} max z = 20 x_{1} + 10 x_{2} + 0 x_{3} + 0 x_{4} \\ s.t. x_{1} - x_{2} + x_{3} = 1 \\ 3 x_{1} + x_{2} + x_{4} = 7 \\ x_{i} \geq 0, i = 1, 2, 3, 4 \end{array}

first change the shape of the problem:

\begin{matrix} z - 20 x_{1} - 10 x_{2} - 0 x_{3} - 0 x_{4} = 0 \\ s.t. \\ x_{1} - x_{2} + x_{3} = 1 \\ 3 x_{1} + x_{2} + x_{4} = 7 \\ x_{i} \geq 0, i \in [1, 4] \end{matrix}

Q: which one of the decision variables must be increased so that objective value increases ? ( in other words, words we have to select one of the non-basic vairables, whos value is currently zero, if we increase the value of one of the basic variables, which gives you increase in the objective value?)

We can see this from the objective function,

Either from

\begin{matrix} max z = 20 x_{1} + 10 x_{2} + 0 x_{3} + 0 x_{4} \end{matrix}

or from

\begin{matrix} z - 20 x_{1} - 10 x_{2} - 0 x_{3} - 0 x_{4} = 0 \end{matrix}

For example:

if we increase the value of x1, from zero to 1, let’s say then z=20.
if we increase the value of x2, which is currently zero, to 1, then z=10.

Each unit increase in the

x1 in crease in z in the 20 units,
x2 ……………………………… 10 units.

Now, in each iteration in the simplex method, we select one of the non-basic variables (current value is zero), and increase the values of the non-basic values to the positive values so that one of them becomes basic.

But this means that, one of the basic variables, must become non-basic. ( we can have only two variables non-basic and only two basic in our case)

First Hypothesis (x1=0,x2=0)

\begin{matrix} x_{1} = 0, \\ x_{2} = 0, \\ x 1 - x 2 + x 3 = 1 \to x 3 = 1 \\ 3 x_{1} + x_{2} + x_{4} = 7 \to x_{4} = 7 \end{matrix}

\begin{matrix} ∴ z = 20 x_{1} + 10 x_{2} + 0 x_{3} + 0 x_{4} \\ z = 0 \end{matrix}

Which is the point C (0,0)

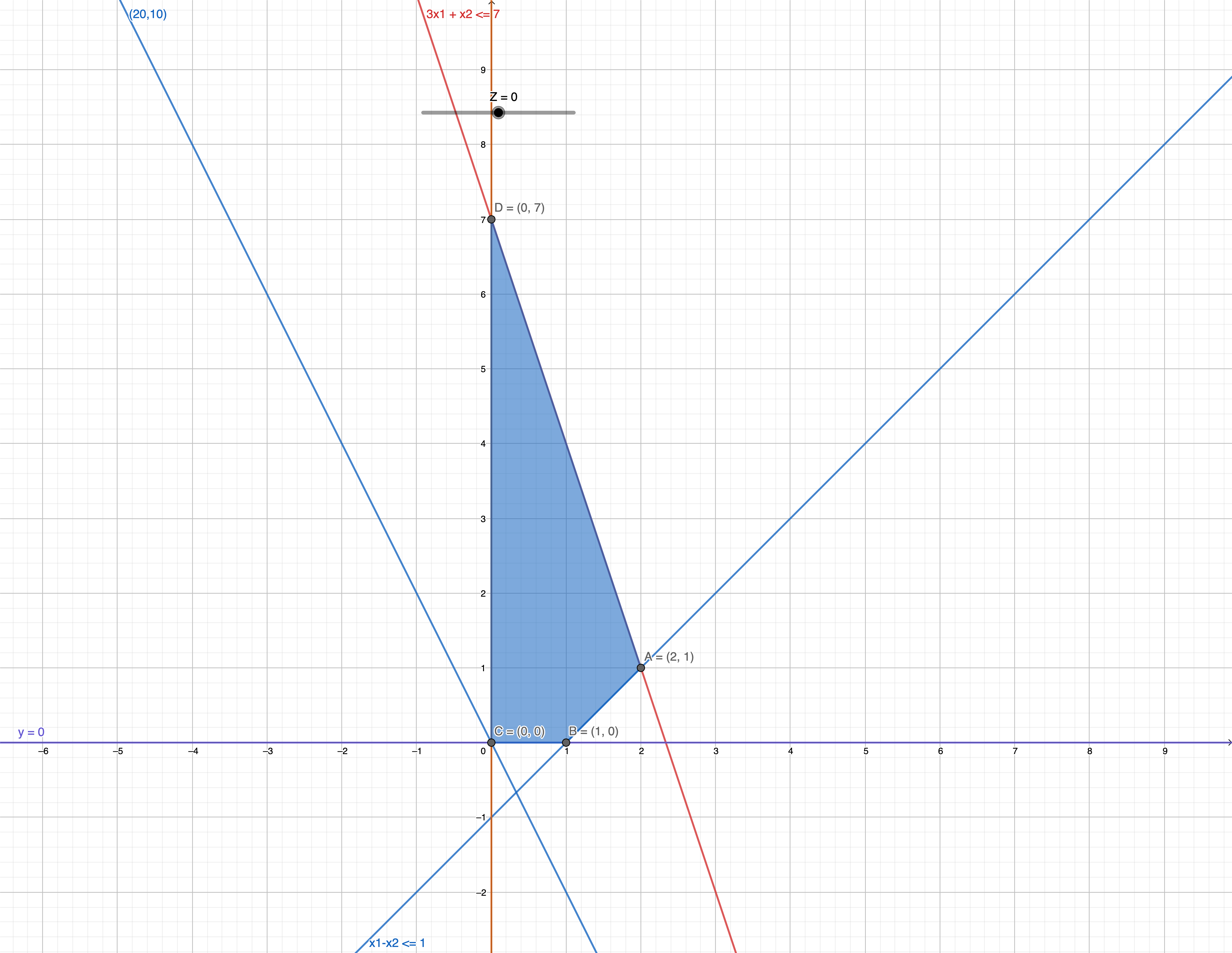
Second Hypothesis (1,0,0,4)

Now, which of the basic variables will become non-basic? ( x3 or x4 ?)

We use the algebric check, the algebrick check is the following:

We determined that x1 should assume positive values.
if we give x1 positive values, what is the largest value we can give to the x1 so that the constraints still satisfies?

In the first constraint :

for example, if we give x1 the value of 1.1

then we have:

\begin{matrix} x_{1} - x_{2} + x_{3} = 1 \\ - 0 + x_{3} = 1 - 1.1 = - 0.1 \end{matrix}

but because all x should be non-negative so, the constraints dose not satisfy, so the maximum number we can give to x1 is 1 then we have x3=0.

In the second constraint:

\begin{matrix} 3 x_{1} + x_{2} + x_{4} = 7 \end{matrix}

we have x2 =0

x_{1} + x_{4} = 7

so the largest number we can give to x1 is 7, in such case x4 = 0

If we consider both of them, what is the largest number we can give to x1 ?

So in order to satisfy both constraints, the maximum value can be given to x1 is min(max_1,max_2 that is min(1,7) = 1

In other words we have to take the minimum.

We forced x1 to be positive , so one of the current positive values (x3,x4) must become zero.

Which of the x3 or x4 should become 0 ?

Now we have :

x_{1} = 1, x_{2} = 0

which of the basic variables should be forced to zero?

we calcualted that, x1 is 1 then we have x3=0.

so we have :

x_{3} = 0,

so :

\begin{matrix} x 1 = 1, x 2 = 0, x 3 = 0, \\ ∵ 3 x_{1} + x_{2} + x_{4} = 7 \\ ∴ 3 + 0 + x_{4} = 7 \Rightarrow x_{4} = 4 \end{matrix}

So our corresponding z value is :

z = 20 x_{1} + 10 x_{2} + 0 x_{3} + 0 x_{4} = 20

Which is the Point B(1,0 )

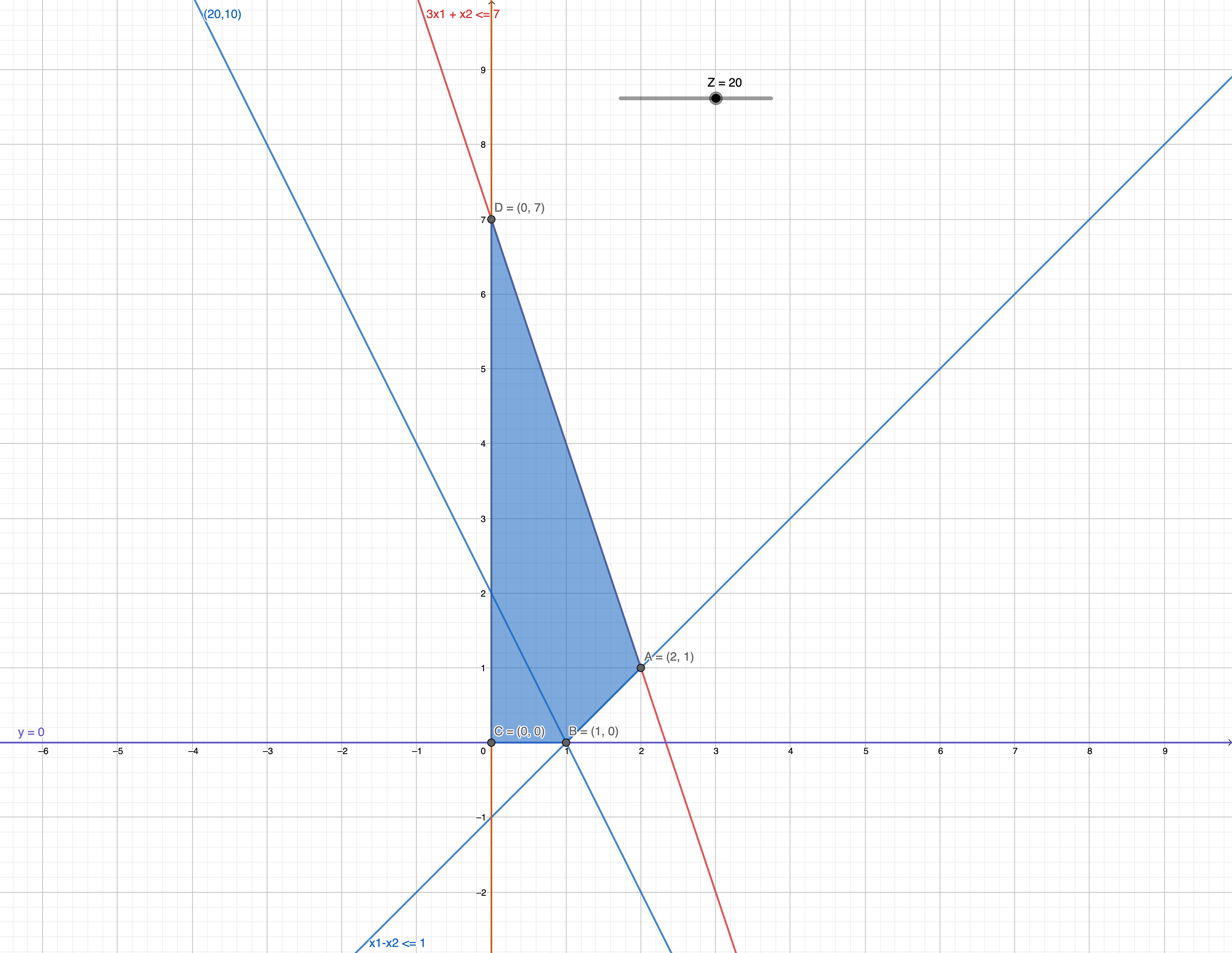
(Matrix) Transformation in the linear system of equations

Solving linear systems with matrices

if we have:

\begin{matrix} A \vec{x} = \vec{b} \\ A A^{- 1} \vec{x} = A^{- 1} \vec{b} \\ I \vec{x} = A^{- 1} \vec{b} \\ \vec{x} = A^{- 1} \vec{b} \end{matrix}

Solving the original problem with matrix notation

We can write the original problem as follows:

\begin{matrix} z - 20 x_{1} - 10 x_{2} - 0 x_{3} - 0 x_{4} = 0 \\ s.t. \\ x_{1} - x_{2} + x_{3} = 1 \\ 3 x_{1} + x_{2} + x_{4} = 7 \\ x_{i} \geq 0, i \in [1, 4] \end{matrix}

x1	x2	x3	x4
-20	-10	0	0	0
1	-1	1	0	1
3	1	0	1	7

So that, we can get, x1 = x2 = 0, x3 = 1, x4 = 7. z = 0 (C)

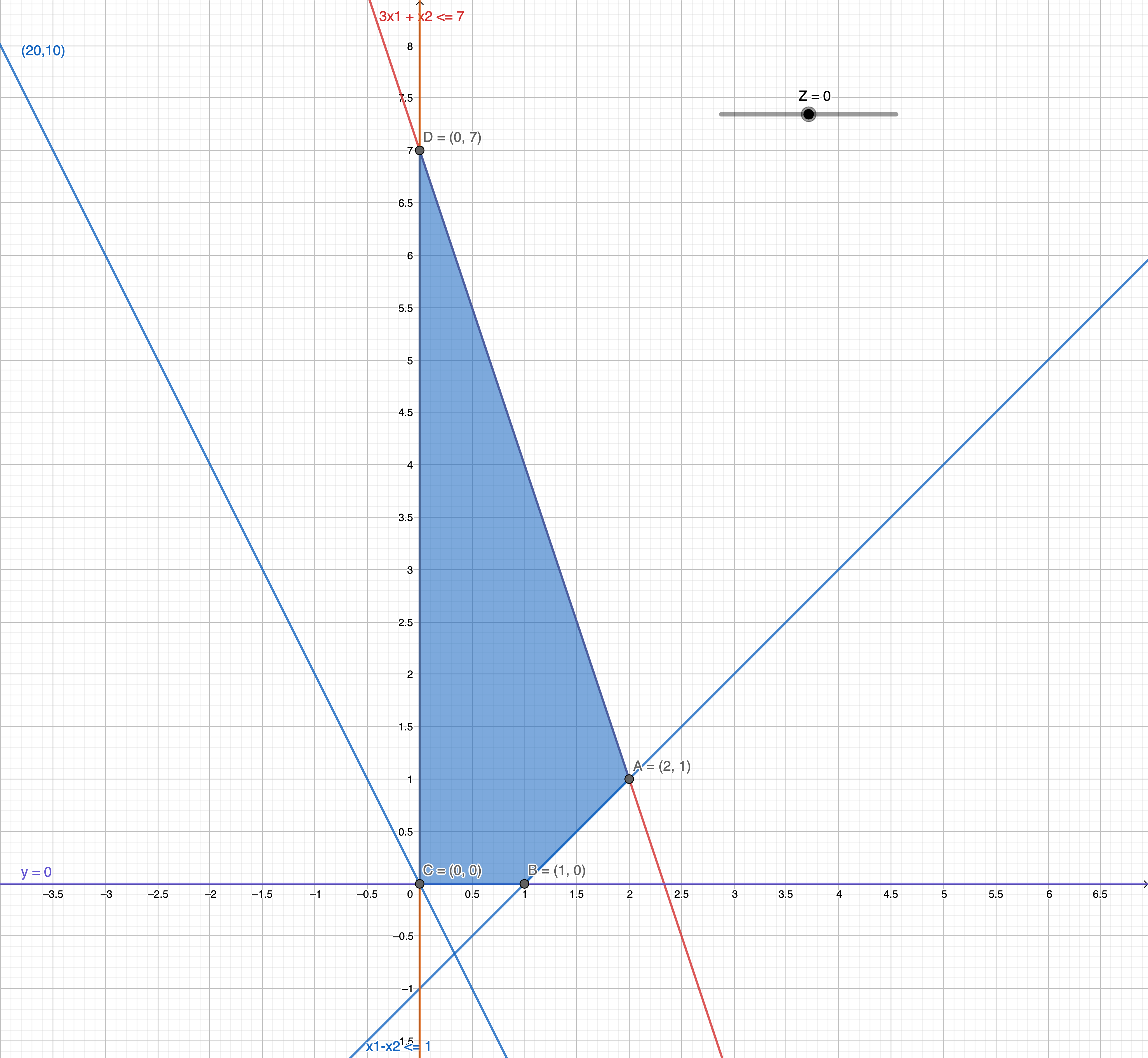
This time we select x1 to be become basic and x3 to be non basic.

x1	x2	x3	x4
0	-30	20	0	20
1	-1	1	0	1
0	4	-3	1	4

z=20 (B)

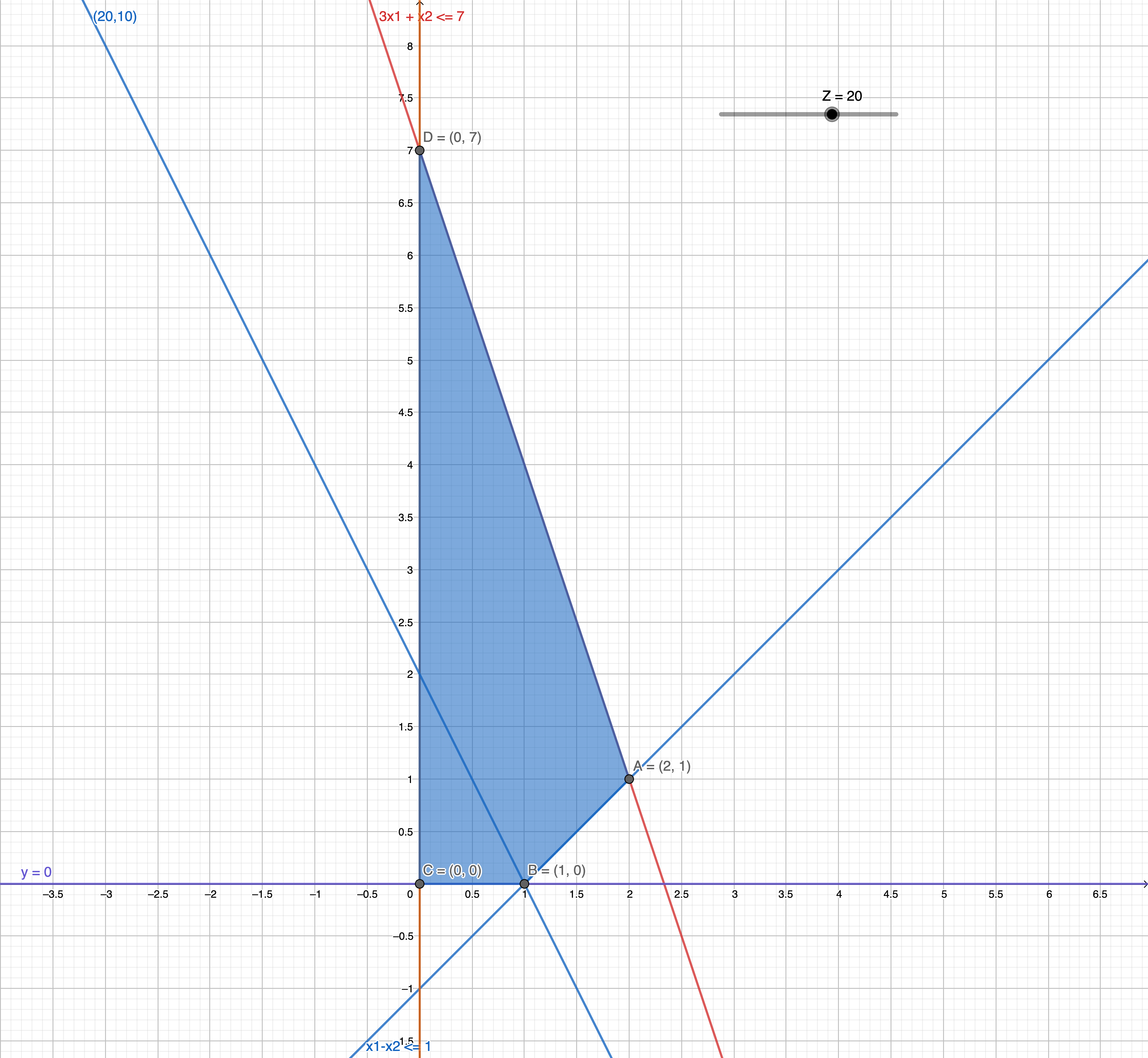
We select x2 this time. and because r1 is negative , we select r4.

x1	x2	x3	x4
0	0	-2.5	7.5	50
1	0	1/4	1/4	2
0	1	-3/4	1/4	1

z = 50 (A)

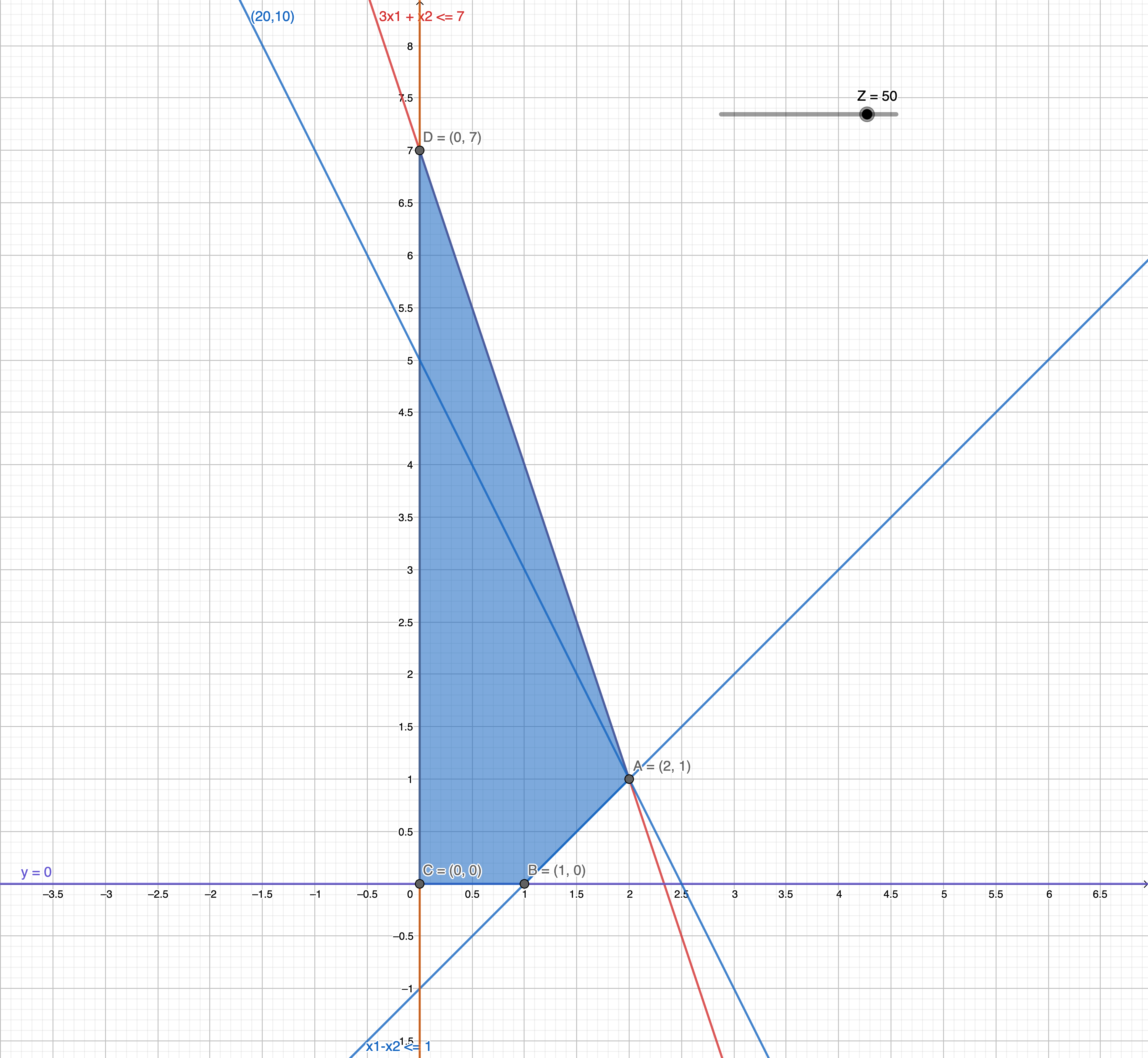
In a maximization problem. there is a negative value in the row of the objkective function, we continue. And also -2.5 is an indicator for us that x3 must become a basic variable this time.

x1	x2	x3	x4
10	0	0	10	70
4	0	1	1	8
3	1	0	1	7

z = 70 (D)

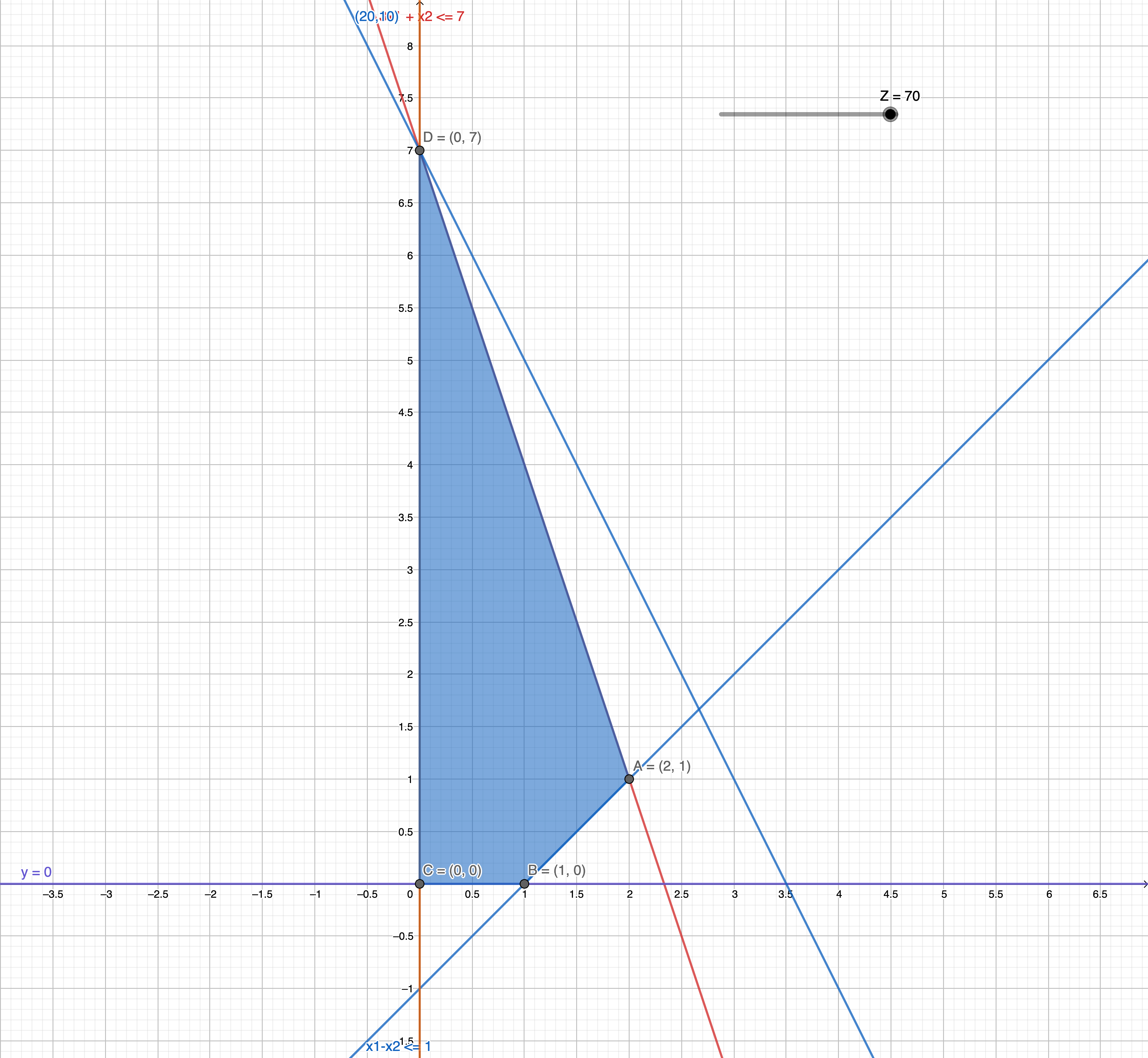
Short - term finance Problem

Notice: Moved to the 1026 Note.

Extra - Answers to the Book Excersises

Exercise 2.1

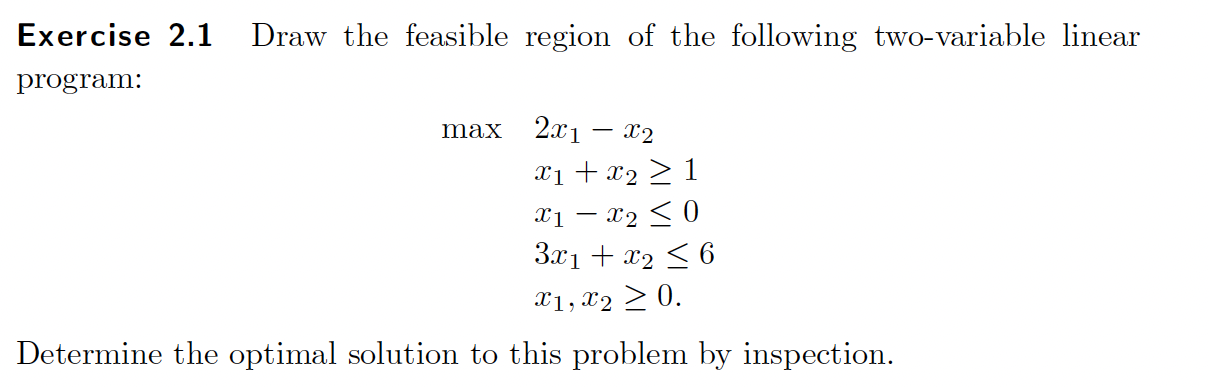
CleanShot 2022-10-28 at 10.05.56

Draw all constraint lines as shown: where

\begin{matrix} e q 1 = x_{1} + x_{2} = 1 \\ e q 2 = x_{1} - x_{2} <= 0 \\ e q 3 = 3 x_{1} + x_{2} = 6 \end{matrix}

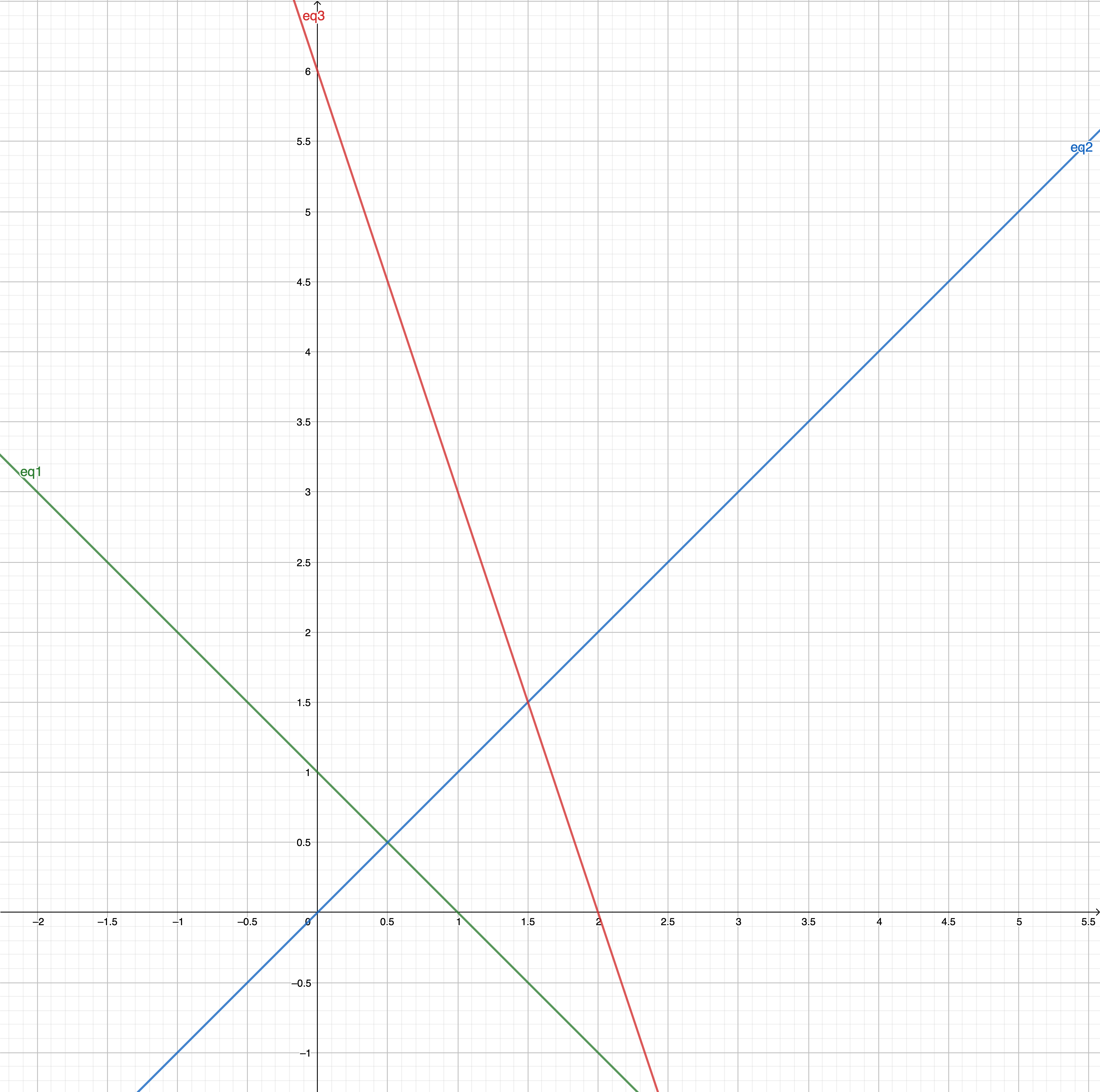
Get all intersection points

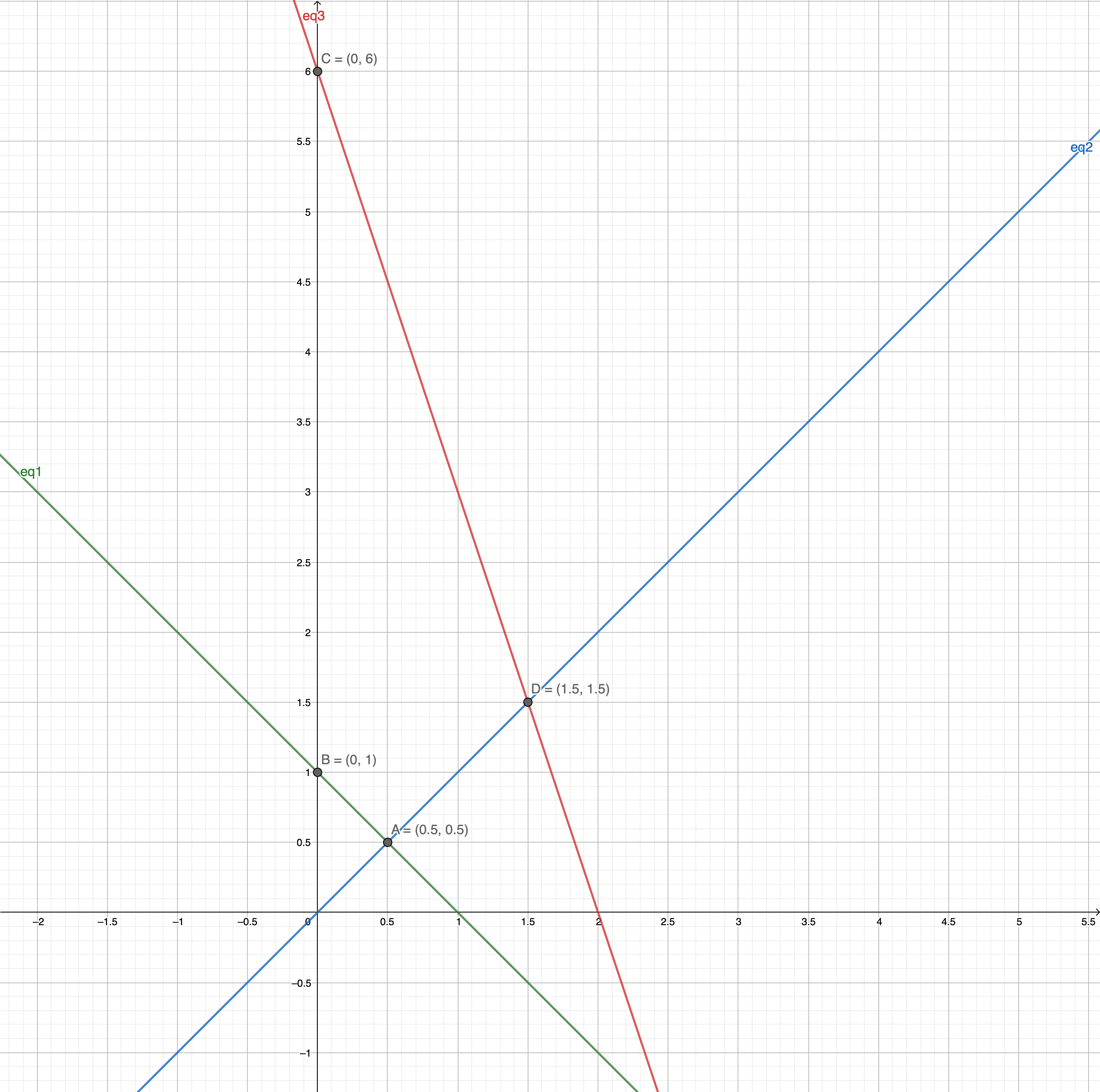
Draw the feasible area

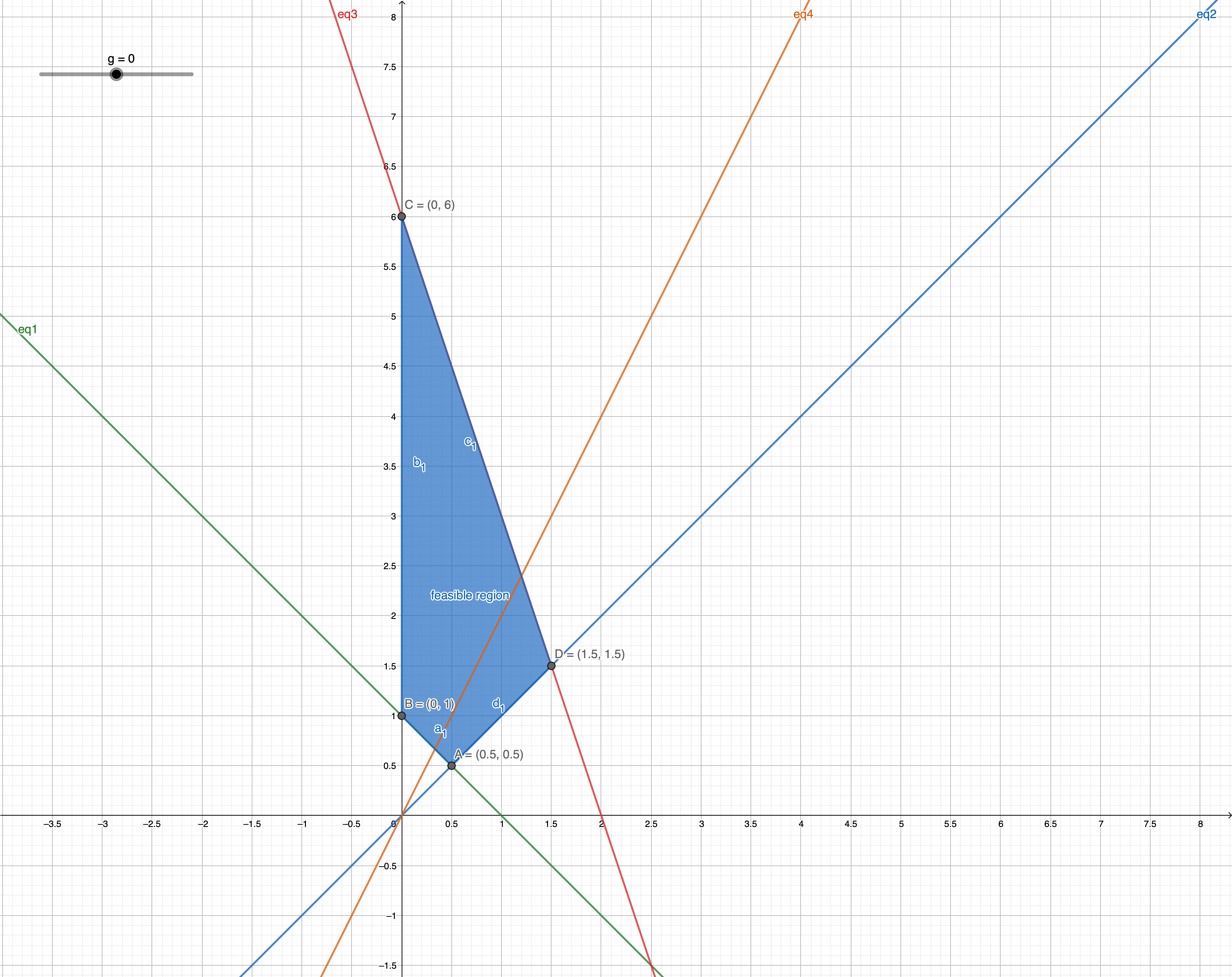
where we have:

e q 4 = 2 x_{1} - x_{2}

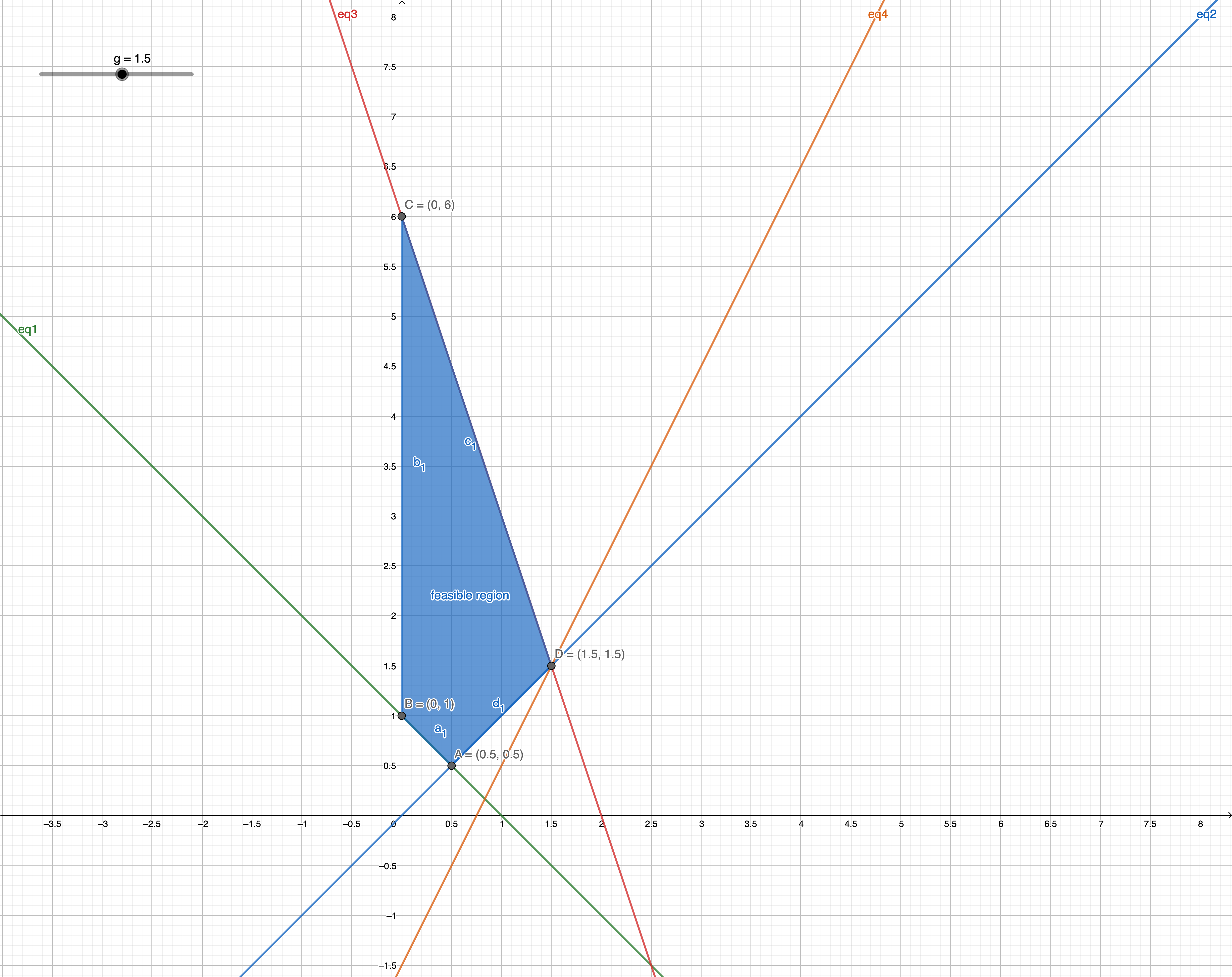
eq4 goes to maximum at point D.

Exercise 2.2

CleanShot 2022-10-28 at 12.40.34

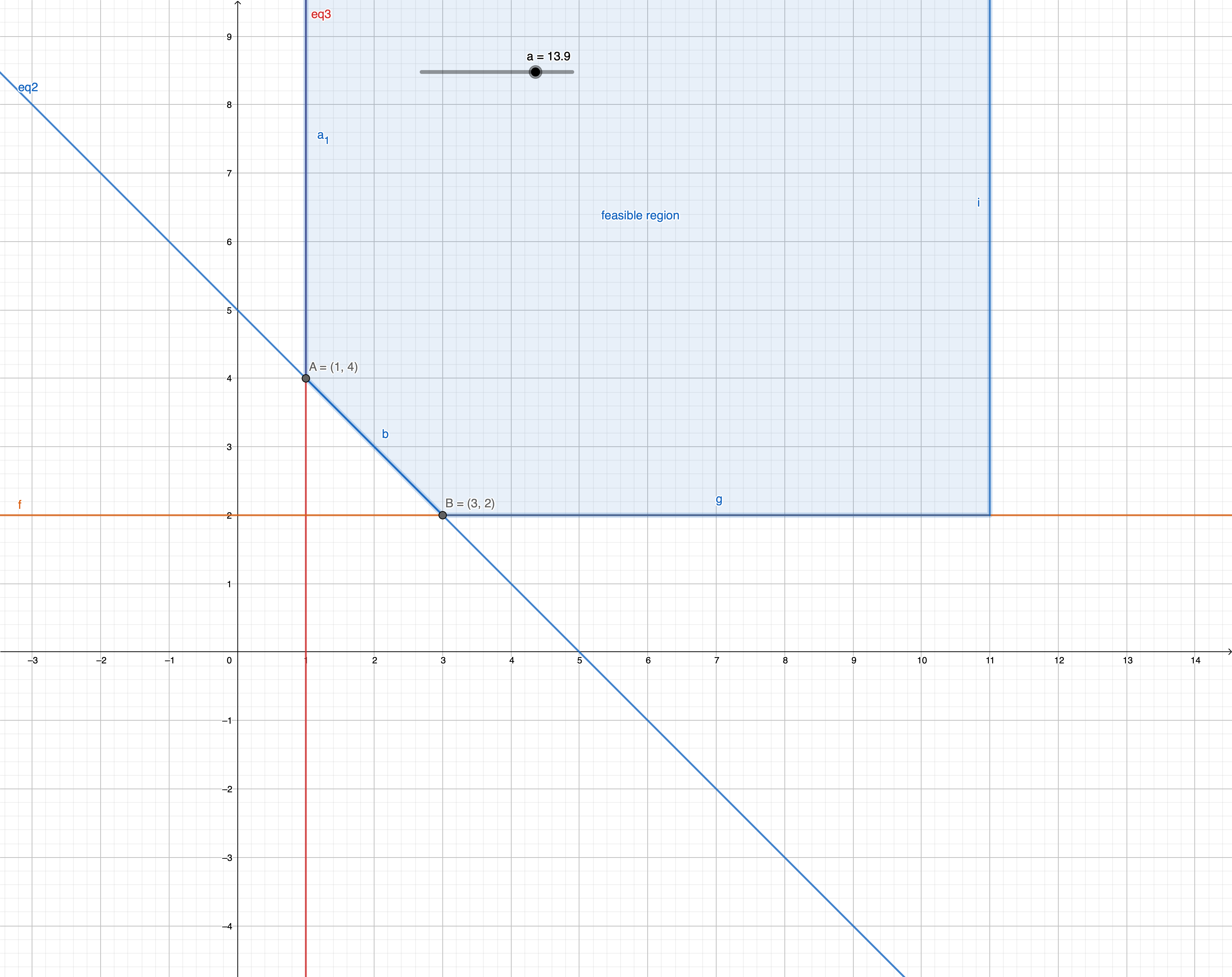
by drawing the feasible region, we can find that , feasible region goes infinite, so the minimum values of the problem occurs at either B and A.

because we have:

\begin{matrix} θ 1 = - 1 \\ θ 2 = - \frac{2}{3} \\ ∴ ∥ θ 2 ∥ < ∥ θ 1 ∥ \end{matrix}

we can find that, minimum value of the Z will be at point B, where

\begin{matrix} Z = 2 \times 3 + 3 \times 2 = 12, \\ \forall x_{1}, x_{2} \in b, \\ Z (x_{1}, x_{2}) \geq Z (3, 2), \end{matrix}

We can also prove this with graphical solution:

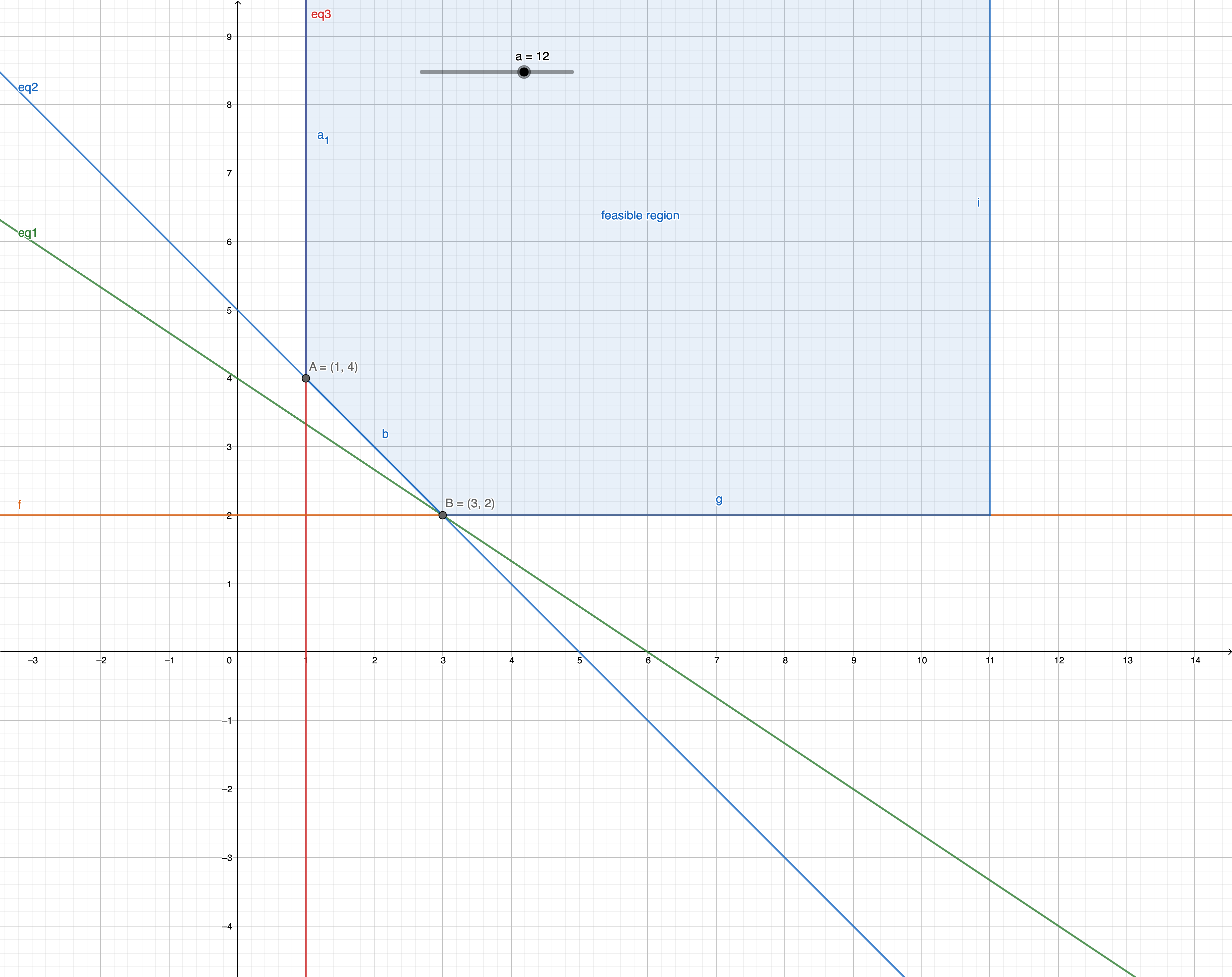
Exercise 2.3 **

CleanShot 2022-10-28 at 13.11.35

Fro mthe given we have:

\begin{matrix} primal: \\ max c^{T} x \\ A x \leq b \\ x \geq 0 \\ ∴ dual: \\ min b^{T} y \\ A^{T} y \leq c \\ y \geq 0 \end{matrix}

Exercise 2.4

CleanShot 2022-10-28 at 21.11.20

A linear program is infeasible if there exists no solution that satisfies all of the constraints -- in other words, if no feasible solution can be constructed.

Example:


4
1
min: x + y;
2
c1: x >= 6;
3
c2: y >= 6;
4
c3: x + y <= 11;


4
1
max: x+y 
2
c1: -x+y <=2
3
c2: x>=0
4
c3: y>=0

Exercise 2.5 **

CleanShot 2022-10-28 at 21.13.28