FE501 – 1214 Nonlinearp Programming Week 3

Calculation of the Hessian Matrix

Calculating PMi to show the type of the Hessian Matrix, which is needed to find whether the function $f(x_1,x_2,..x_n)$$f(x_1,x_2,..x_n)$ is a convex, concave or neither.

Expl. $f(x,y)=x^2-y^2$$f(x,y)=x^2 - y^2$

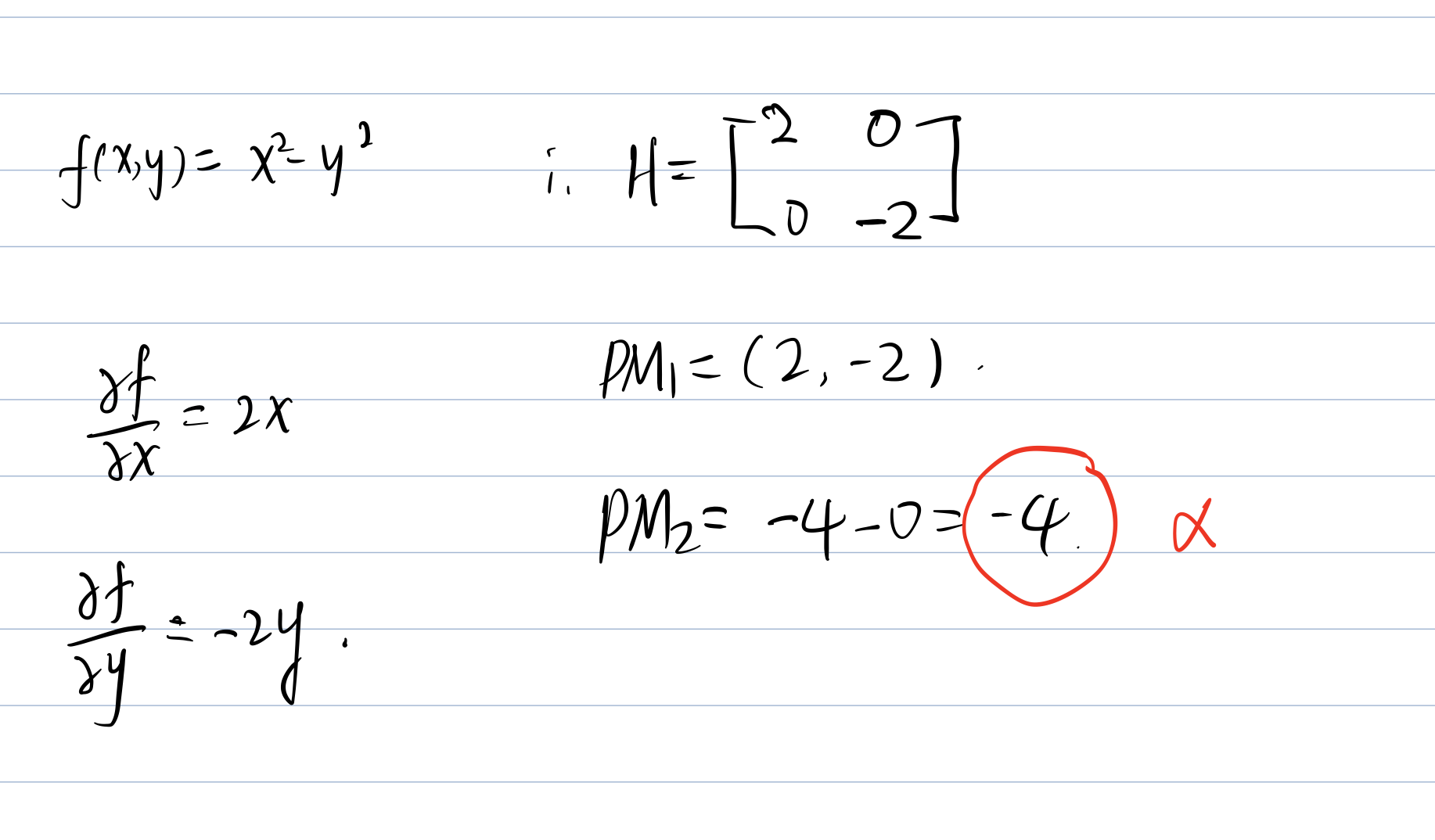
Note: First order PMs are on the diagnoze. Second is the determinate of the matrix.

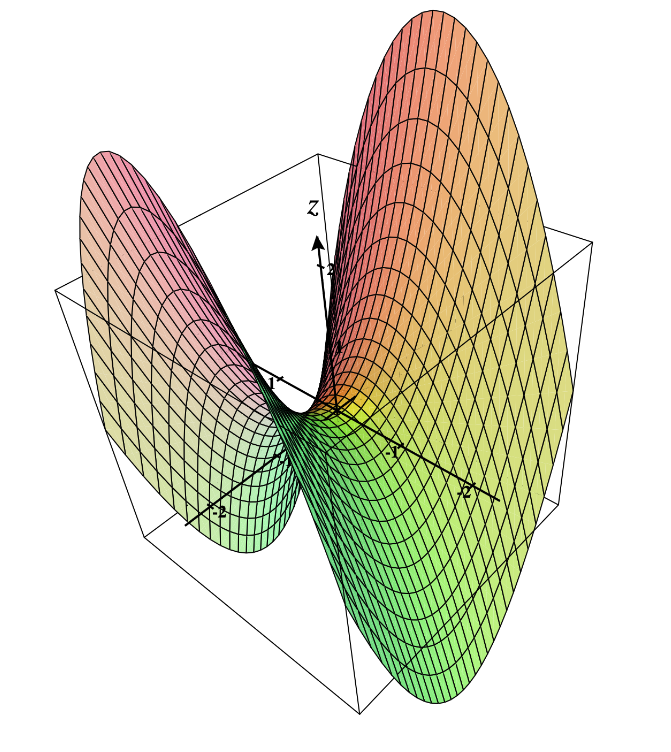
The function is Neither Convex Nor Concave (NCNC)

Expl. $f(x,y)=x^2+y^2$$f(x,y)=x^2 + y^2$

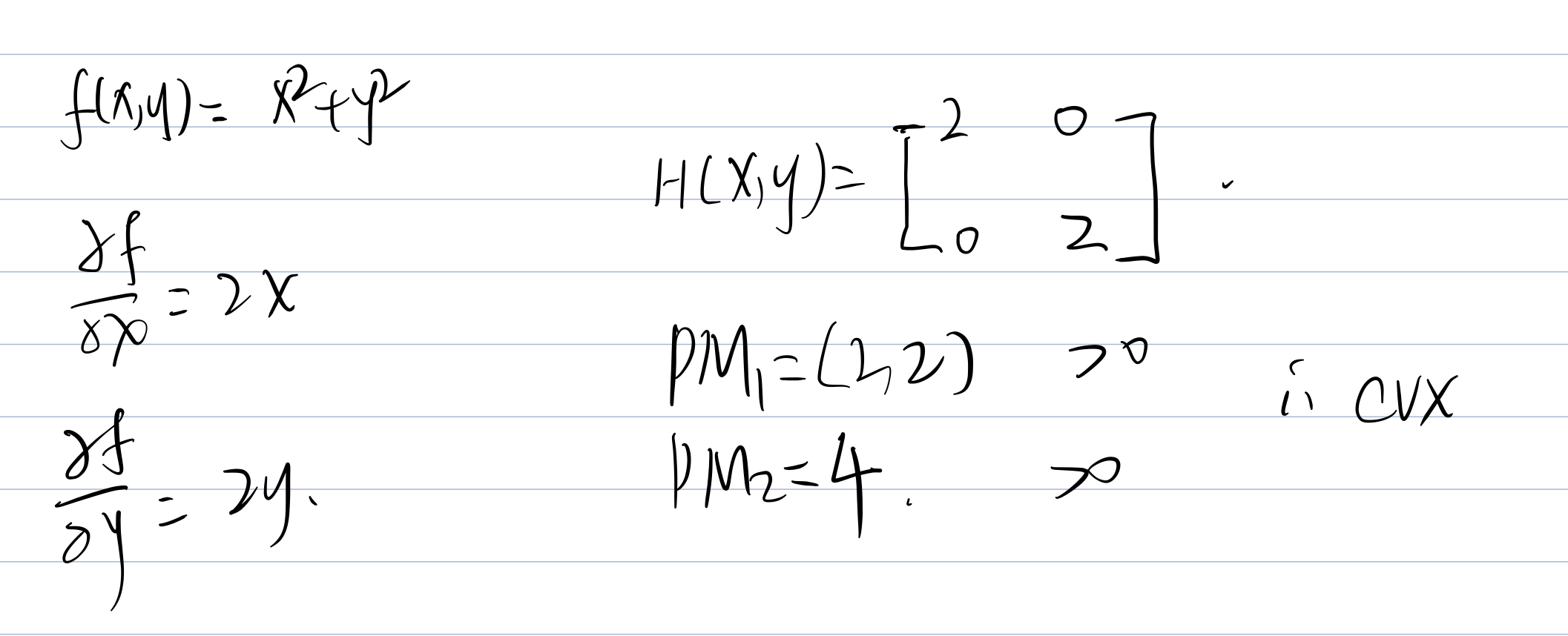
Actually we do not need to calculate this, because:

1. Sum of CVX is CVX.
2. Sum of CCV is CCV
3. if $f(\overrightarrow{x})$$f(\vec x)$ is CVX, then $-f(\overrightarrow{x})$$-f(\vec x)$ is CCV

Expl. $f(x,y)=-x^2-y^2$$f(x,y)=-x^2 - y^2$

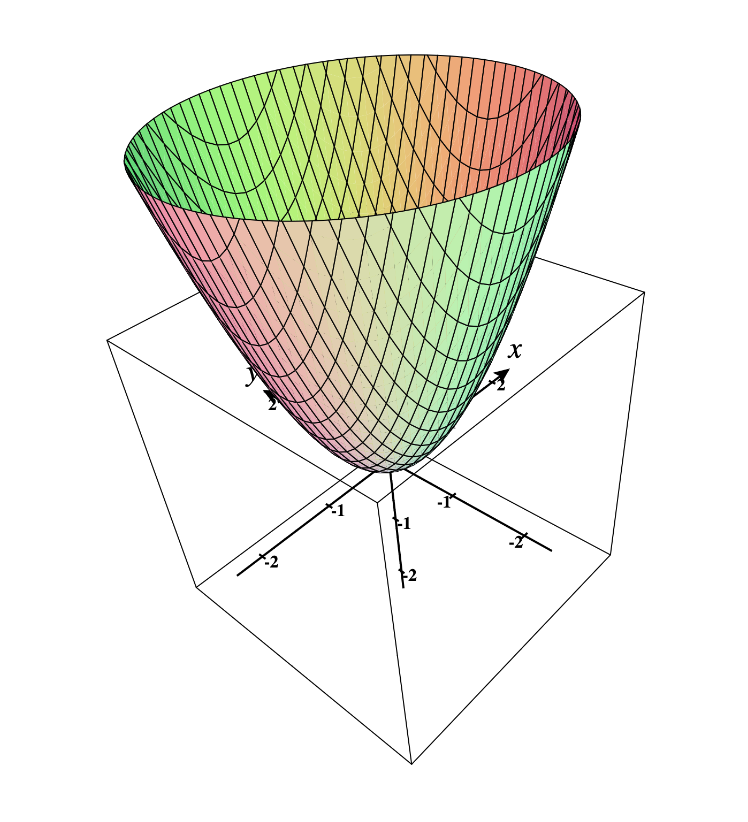
This is CCV (concave) cause sum of CCV is CCV.

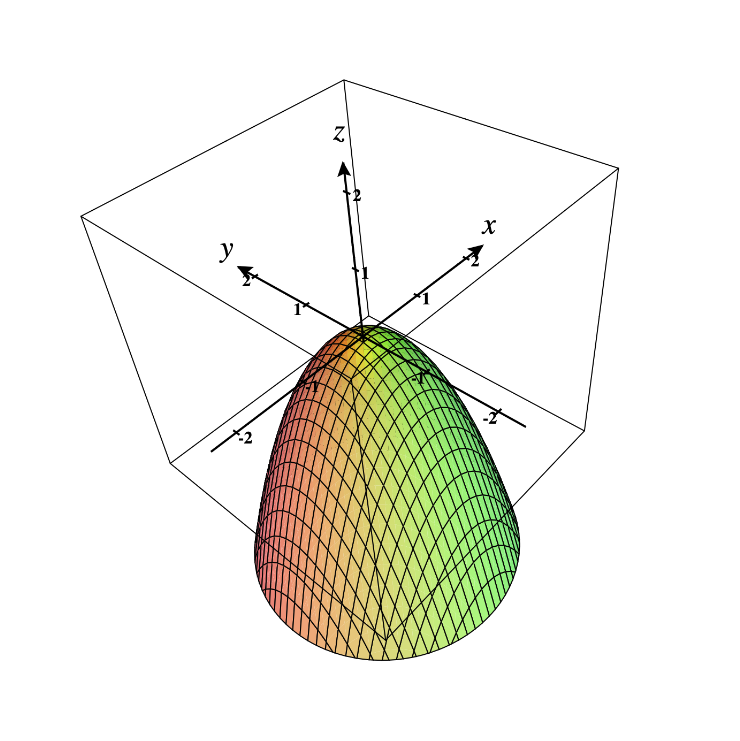
Expl. $f(x,y)=x^2+y^2+xy$$f(x,y)=x^2 + y^2 + xy$

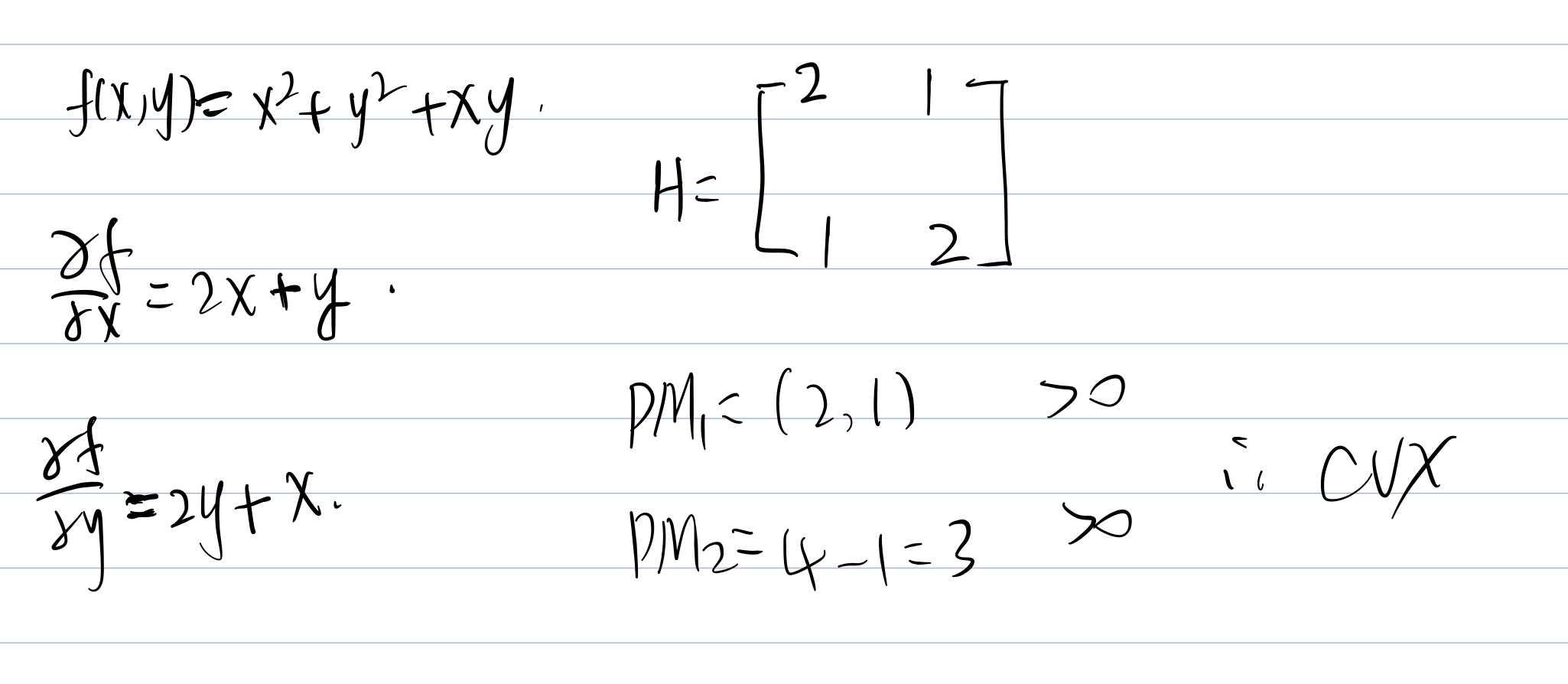
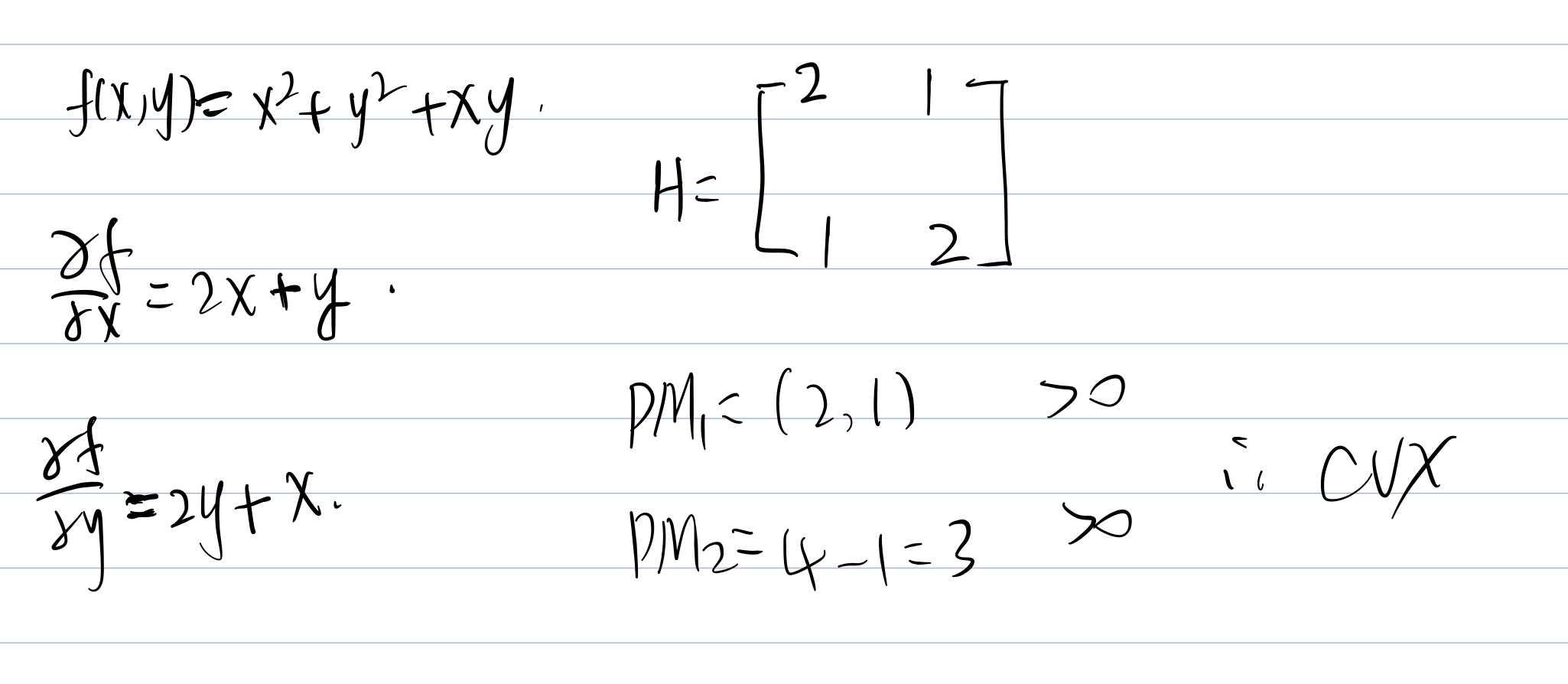
Expl. $f(x,y)=-x^2-y^2-xy$$f(x,y)=-x^2 - y^2 - xy$

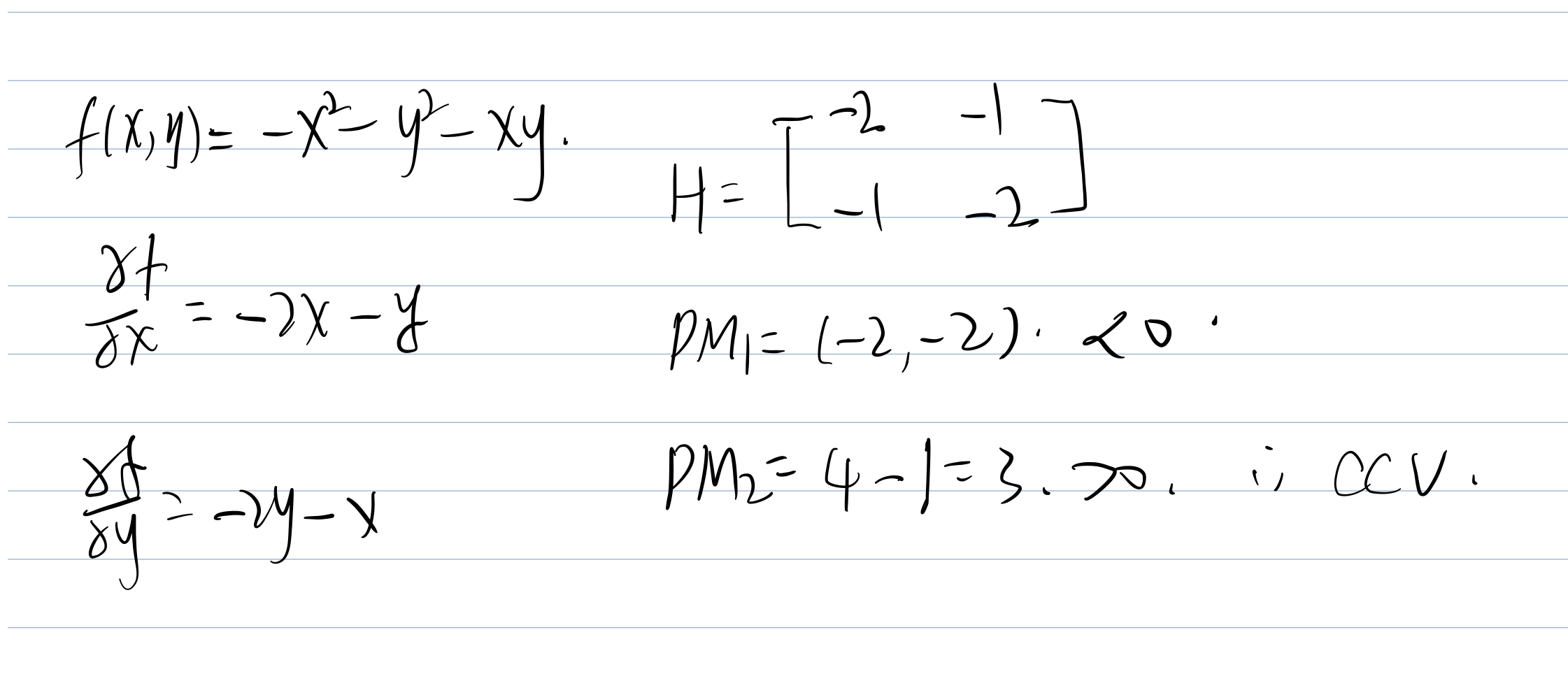
NOTICE: Wrong result is addressed on this problem during the class!

Unconstrained Nonlinear Optimization Problems

B.N.11.6-655

We now discuss how to find an optimal solution (if it exists) or a local extremum (local optimum point) for the following unconstrained NLP:

We assume that for the given function the first and second partial derivatives are all exists.

Gradient and Stationary Point

Let $\frac{\partial f(\overrightarrow{x})}{\partial x_i}$$\frac{\part f(\vec x)}{\part x_i}$ =

in formula (2) is called the gradient of the function.

Necessary condition for $\overrightarrow{x}=(x_1,x_2,..x_n)$$\vec x = (x_1,x_2,..x_n)$ to be a local extremum for NLP is:

That means, for one dimensional function (single variable function), we just have to check the $f^{\prime }(x)$$f'(x)$ either being zero or not at the point.

Expl. $f(x)=x^2$$f(x)=x^2$

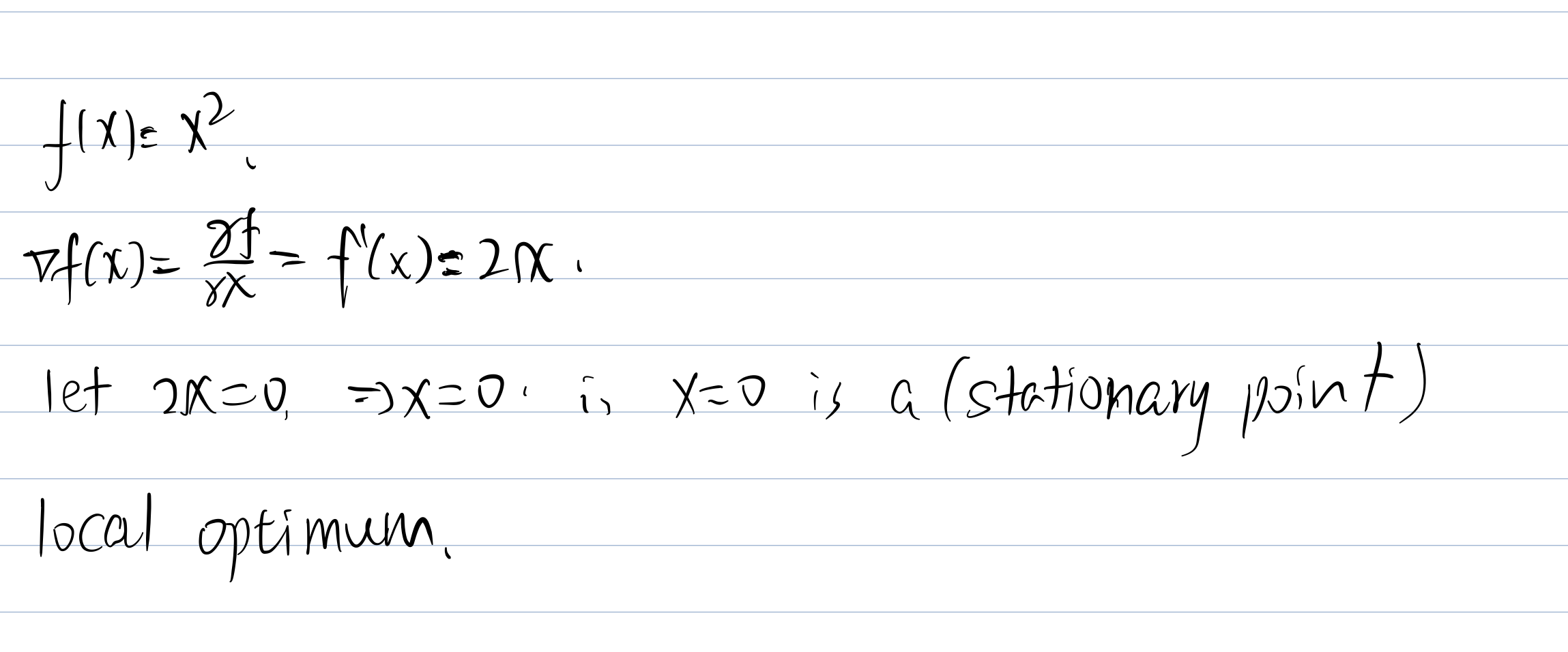
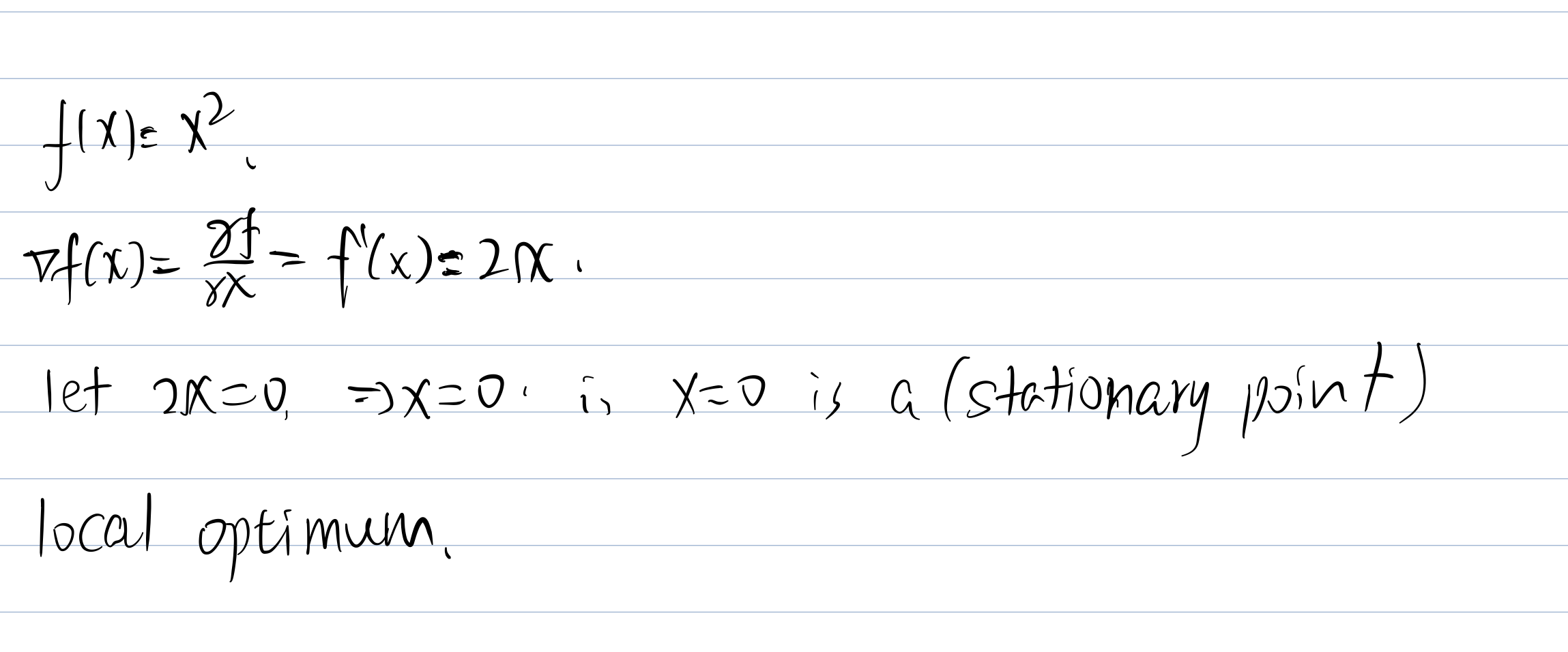
We have learned how to determind the domain being either convex or not, and we also have learned determining the objective function being either convex or not, and now we will start learning about the local maximum or local minimum points and their properties.

Stationary points where gradient of $\mathbf{\nabla }f(\overrightarrow{x})=0$$\grad f(\vec x)=0$ are candidate points for being local optimum solution.

or in other way:

A point $\overrightarrow{x}$$\vec x$ having $\mathbf{\nabla }f(\overrightarrow{x})=0$$\grad f(\vec x)=0$ is called a stationary point of $f$$f$.

More about stationary point (Optional Information¹)

NOTE: you can skip this.

A stationary point, or critical point, is a point at which the curve's gradient equals to zero. Consequently if a curve has equation y=f(x) then at a stationary point we'll always have:

which can also be written:

In other words the derivative function equals to zero at a stationary point*.

Different types of stationary points

There are three types of stationary points:

• local (or global) maximum points
• local (or global) minimum points
• horizontal (increasing or decreasing) points of inflexion.

It is worth pointing out that maximum and minimum points are often called turning points.

Turning points

A turning point is a stationary point, which is can be:

• a local (or global) minimum
• a local (or global) maximum

each of which are illustared in the graphs shown here, where the horizontal tangent is shown in orange:

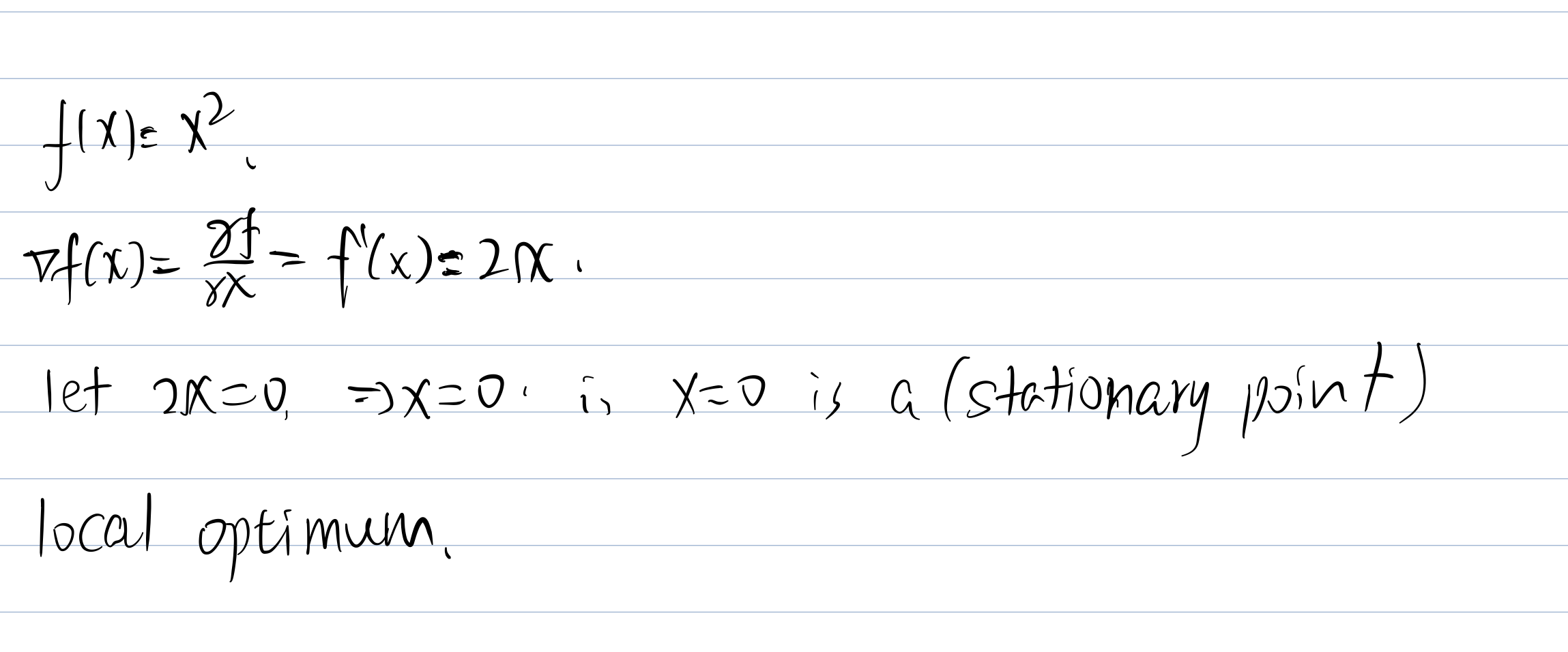
How to find Stationary point ?

Given a function f(x) and its curve y=f(x), to find any stationary point(s) we follow three steps:

• Step 1: find f′(x)
• Step 2: solve the equation f′(x)=0, this will give us the x-coordinate(s) of any stationary point(s).
• Step 3 (if needed/asked): calculate the y-coordinate(s) of the stationary point(s) by plugging the x values found in step 2 into f(x).

Stationary point and Local Minimum or Local Maximum (1)

(Choose either (1) or (2) methods, both has the same meaning but slightly different approach for finding the local minimum or maximum)

As we know that:

A point $\overrightarrow{x}$$\vec x$ having $\mathbf{\nabla }f(\overrightarrow{x})=0$$\grad f(\vec x)=0$ is called a stationary point of $f$$f$.

Let’s say for a given function $f(\overrightarrow{x})$$f(\vec x)$ we found the graph like this:

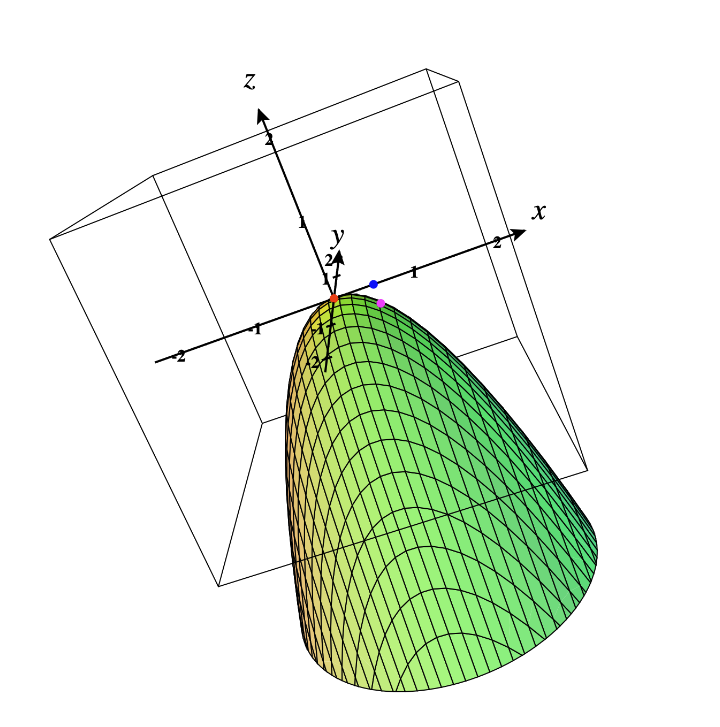
(Apparently this is a CCV function).

As we can see, or let’s say we have calculated the $\mathbf{\nabla }$$\grad$ of the function and found a point $\overrightarrow{x}$$\vec x$ (red point in the graph) which holds $\frac{\partial f(\overrightarrow{x})}{\partial x_i}=0,i=1,2,...n$$\frac{\part f(\vec x)}{\part x_i}=0, i=1,2,...n$ ,

Let’s say when we increase the value of x slightly, without changing the values of y or z on the graph, we got the blue point. the function value for blue point holds:

which also indicates that in it’s neibourhood of point(red), it is a local maximum point by definition.

To observe this more formally, we use Hessian matrix.

For a given stationary point $x^s$$x^s$,

If $H_k(x^s)>0,k=1,2,...n$$H_k(x^s) > 0, k=1,2,...n$, then a stationary point $x^s$$x^s$ is a local minimum point for NLP.

If, for $k=1,2,...n,H_k(x^s)$$k=1,2,...n, H_k(x^s)$ is nonzero, and has the same sign as $(-1{)}^k$$(-1)^k$, then a stationary point $x^{\ast }$$x^*$ is a local maximum for NLP.

If $H_n(x^s)\ne 0$$H_n(x^s) \ne 0$ and the conditions above do not hold, then a stationary point $x^s$$x^s$ is not a local extremum (not a local max or min), if a stationary point $x^s$$x^s$ is not a local extremum, then it is called a saddle point.

If $H_n(x^s)=0$$H_n(x^s)=0$ for a stationary point, then the stationary point may be a local maximum, a local minimum or a saddle point, and the preceding tests are inconclusive.

 

Stationary point and Local Minimum or Local Maximum (2)

This definition and process is given by Hocam and you might find this more useful.

For an unconstrined NLP, stationary points where the gradient $\mathbf{\nabla }f(\overrightarrow{x})=0$$\grad f (\vec x) = 0$ are the candidate points for being a local optimum solution.

Expl. $f(x)=x^2$$f(x) =x^2$

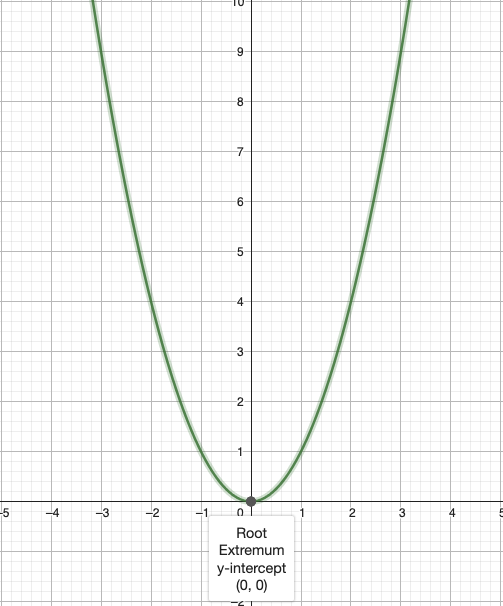
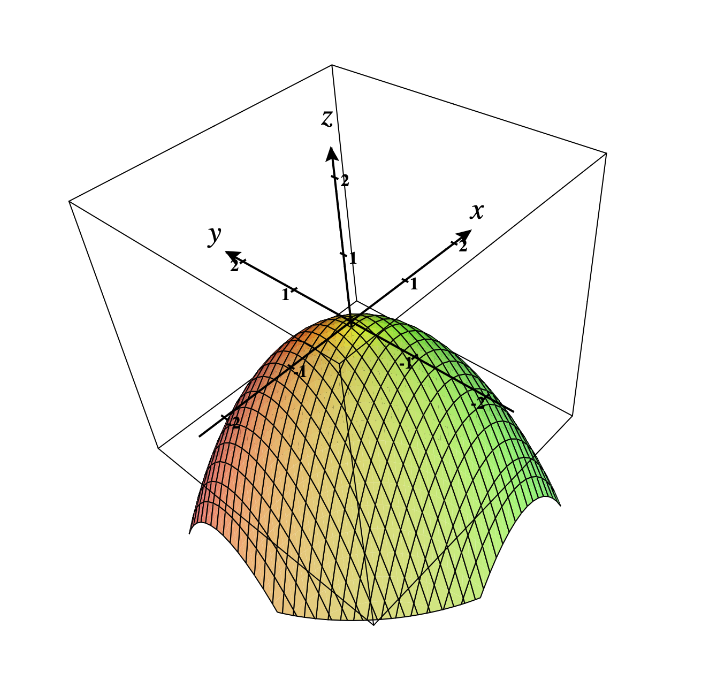
so x=0 is a local optimum point (for this problem it is min).

There are three posibilities:

1. local minimum
2. local maximum
3. inflection point

Expl. $f(x)=-x^2$$f(x)=-x^2$

So for this particular problem, x=0 is a local maximum point.

Expl. $f(x)=x^3$$f(x) = x^3$

But x=0 is not a local maximum nor a local minimum point, it is a inflaction point.

So someother steps are needed in order to determine the type of the point.

Expl. $f(x)=-2x^2$$f(x)=-2x^2$

Expl. $f(x)=x^3$$f(x)=x^3$

Actually, it is a inflaction point.

Expl. $f(x)=x^4$$f(x)=x^4$

Obviously, x=0 is local minimum.

Unconstrained Theorems Theorems

If first non-zero derivative occurs at an odd ordered derivative, then x is an inflaction point.

If first non-zero derivative occurs at an even ordered derivative, and:

2
1
- The value is **positive**, stationary point x is **local minimum**.
2
- The value is **negative**, stationary point x is **local maximum**.

For a convex function, the local minimum is a gloabl minimum.

For a concave function, the local maximum is a global maximum.

In a case that we can not determine the function being convex or concave, then we need to:

• check all the local minimum points and local maximum points
• chec the boundary points of the function domains on the feasible region.

For single variable function (single dimension)

Exercise $f(x)=x^3-2x+3$$f(x) = x^3-2x+3$

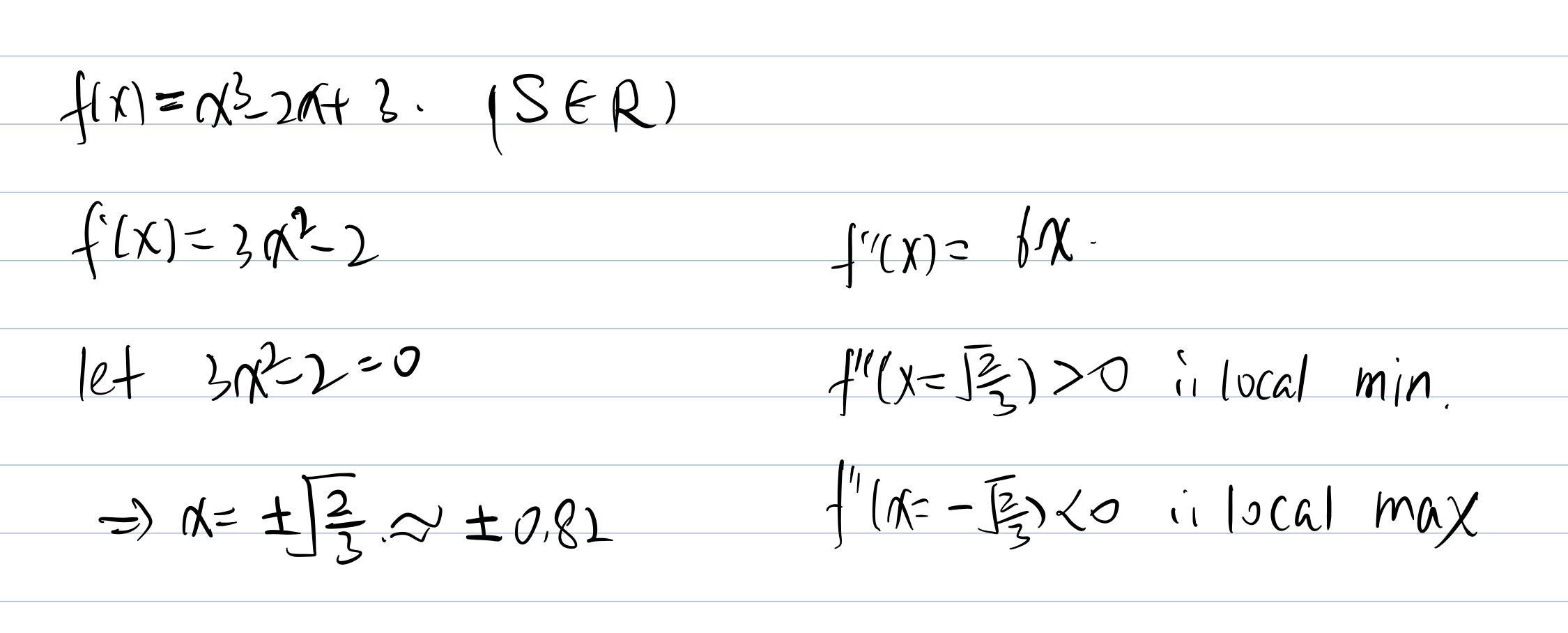
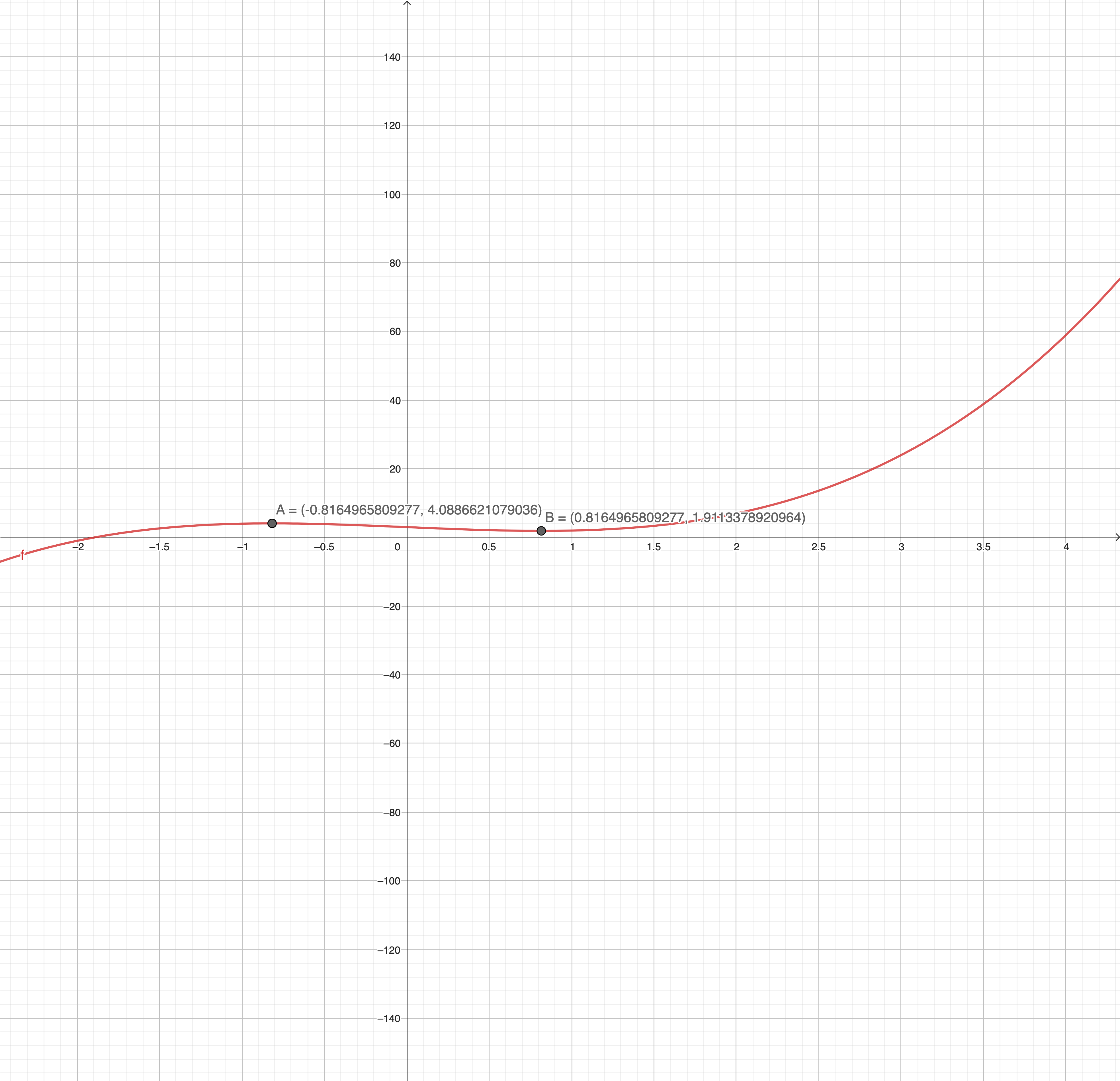
Check the function convexity :

So this function is not convex nor concave.

Now we will test boundaries of the function:

$li{m}_{x\to \mathrm{\infty }}f(x)\to \mathrm{\infty }$$lim_{x\rightarrow\infin}{f(x)} \rightarrow \infin$

$li{m}_{x\to -\mathrm{\infty }}f(x)\to -\mathrm{\infty }$$lim_{x\rightarrow -\infin}{f(x)} \rightarrow -\infin$

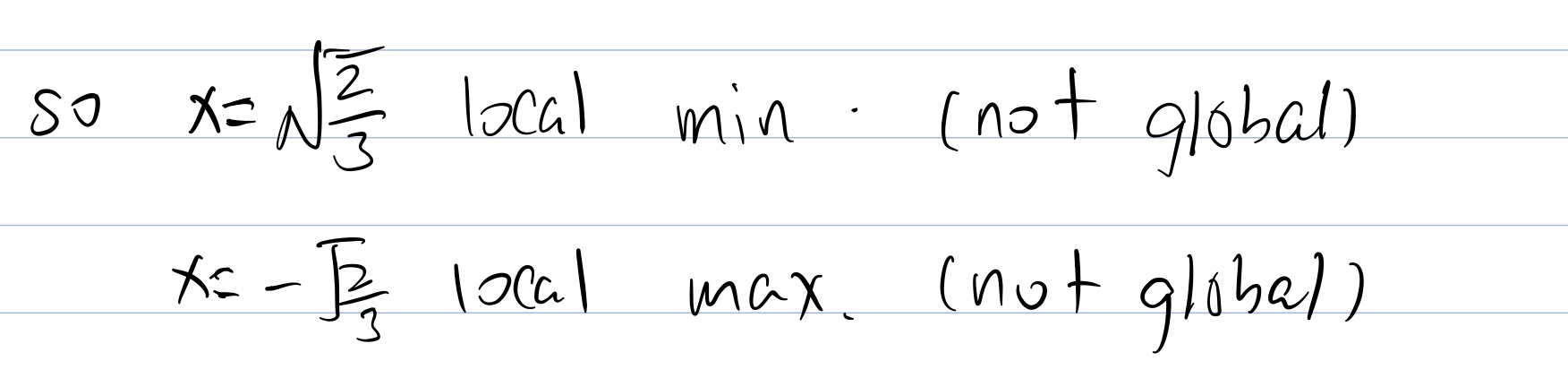
For multi-dimensional function (multivariable function)

Exercise $f(x,y)=x^{2}y+x{y}^3-xy$$f(x,y) = x^2y+xy^3-xy$

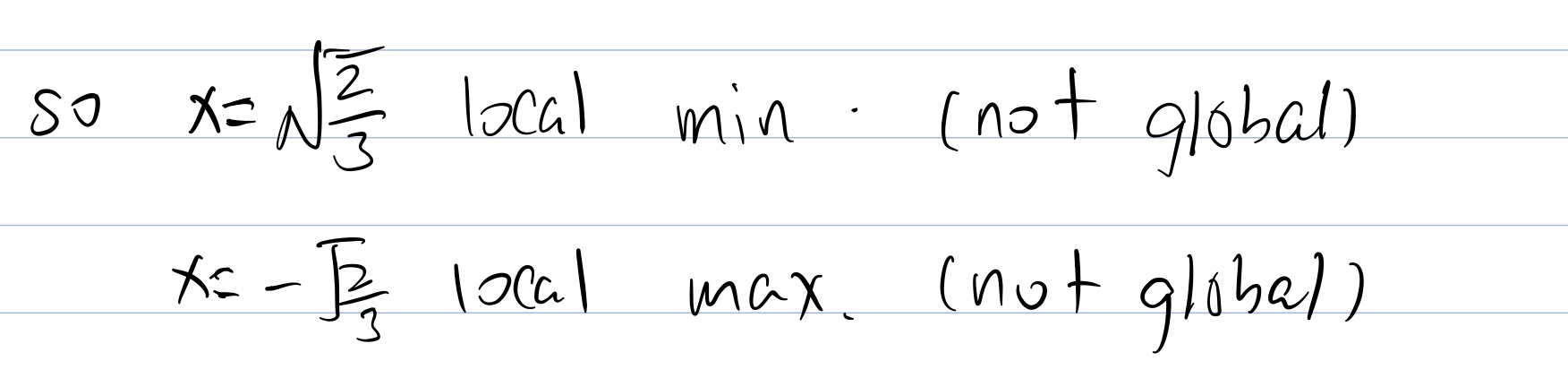
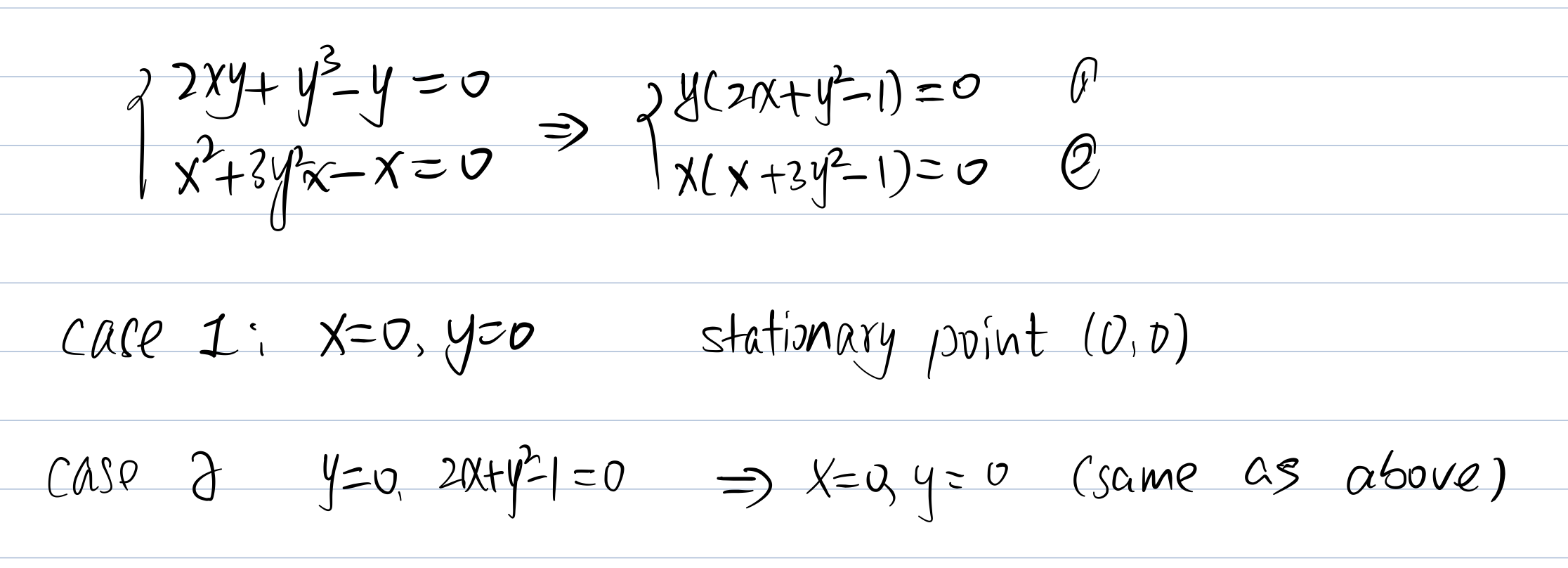
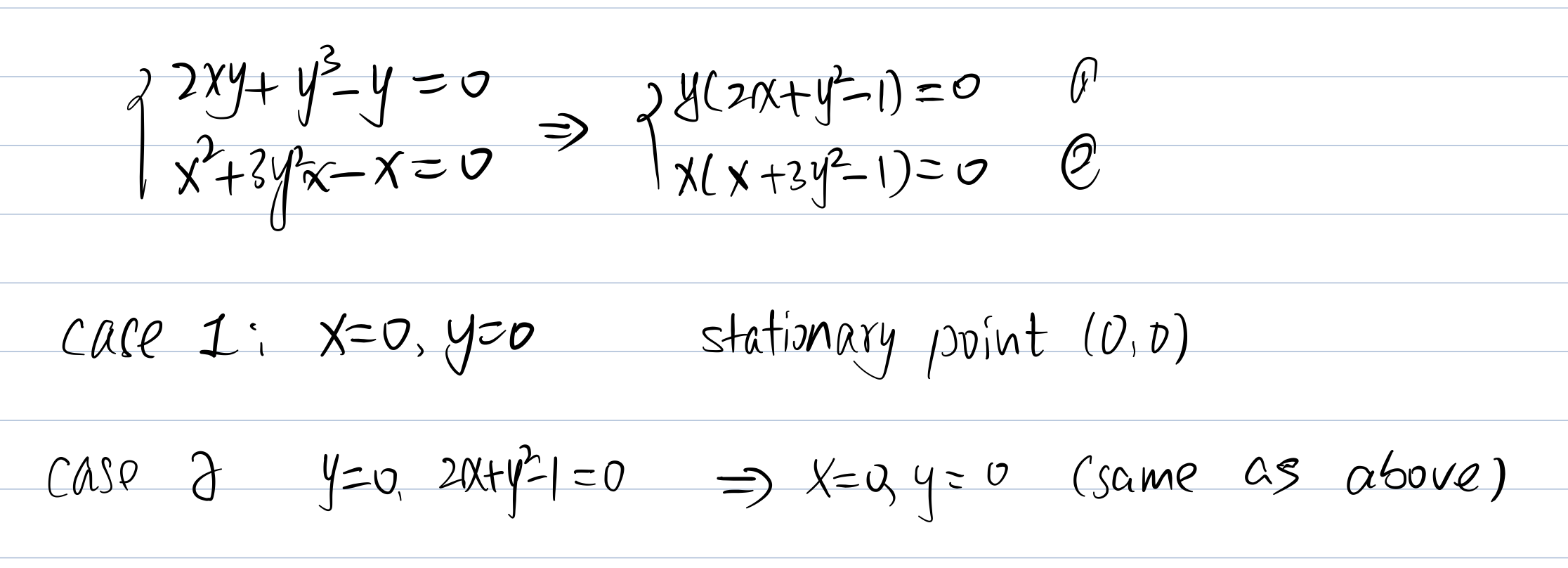
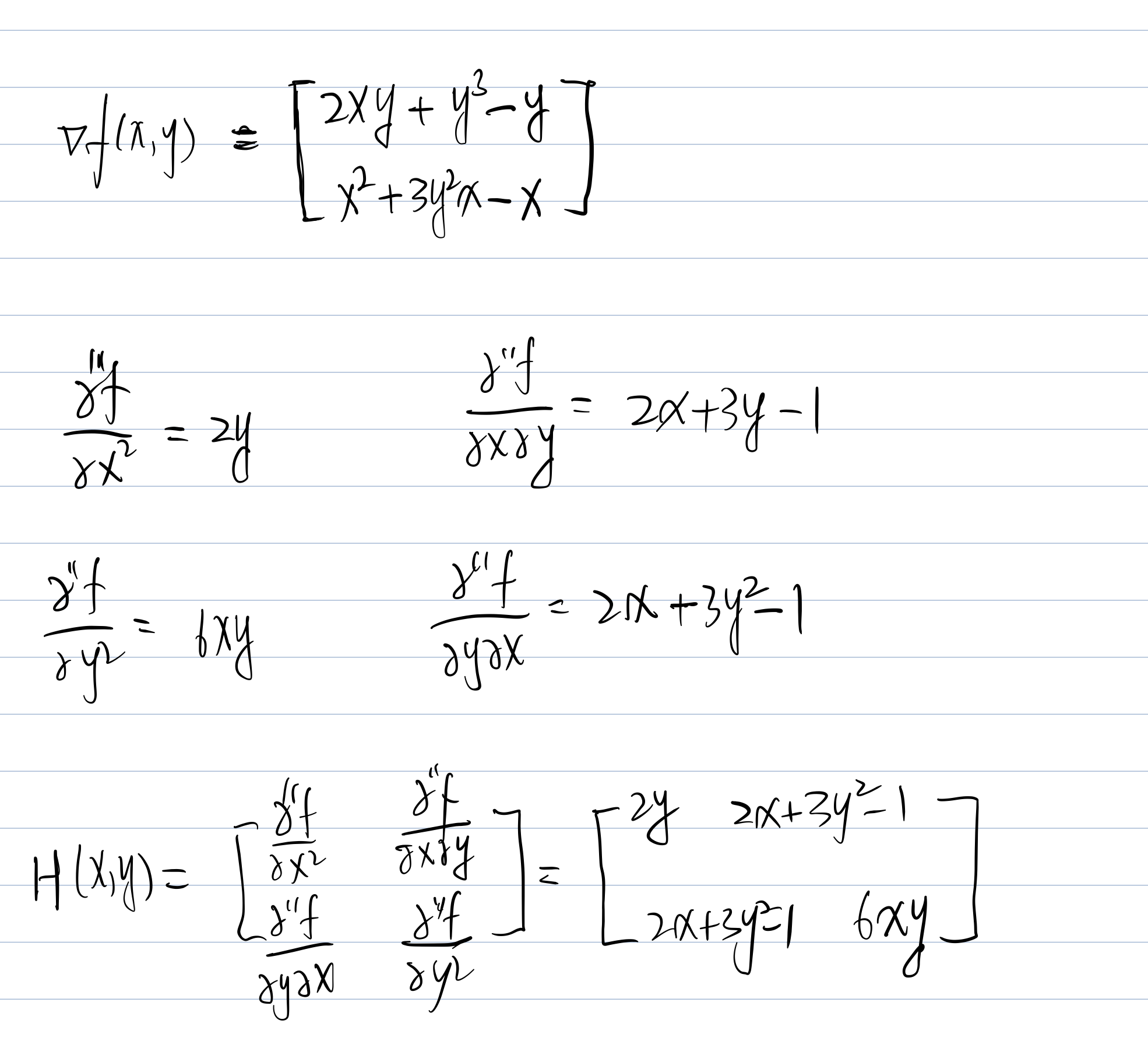
Now we need to put each stationary point into the H(x,y) and check the Hessian Matrix Value.

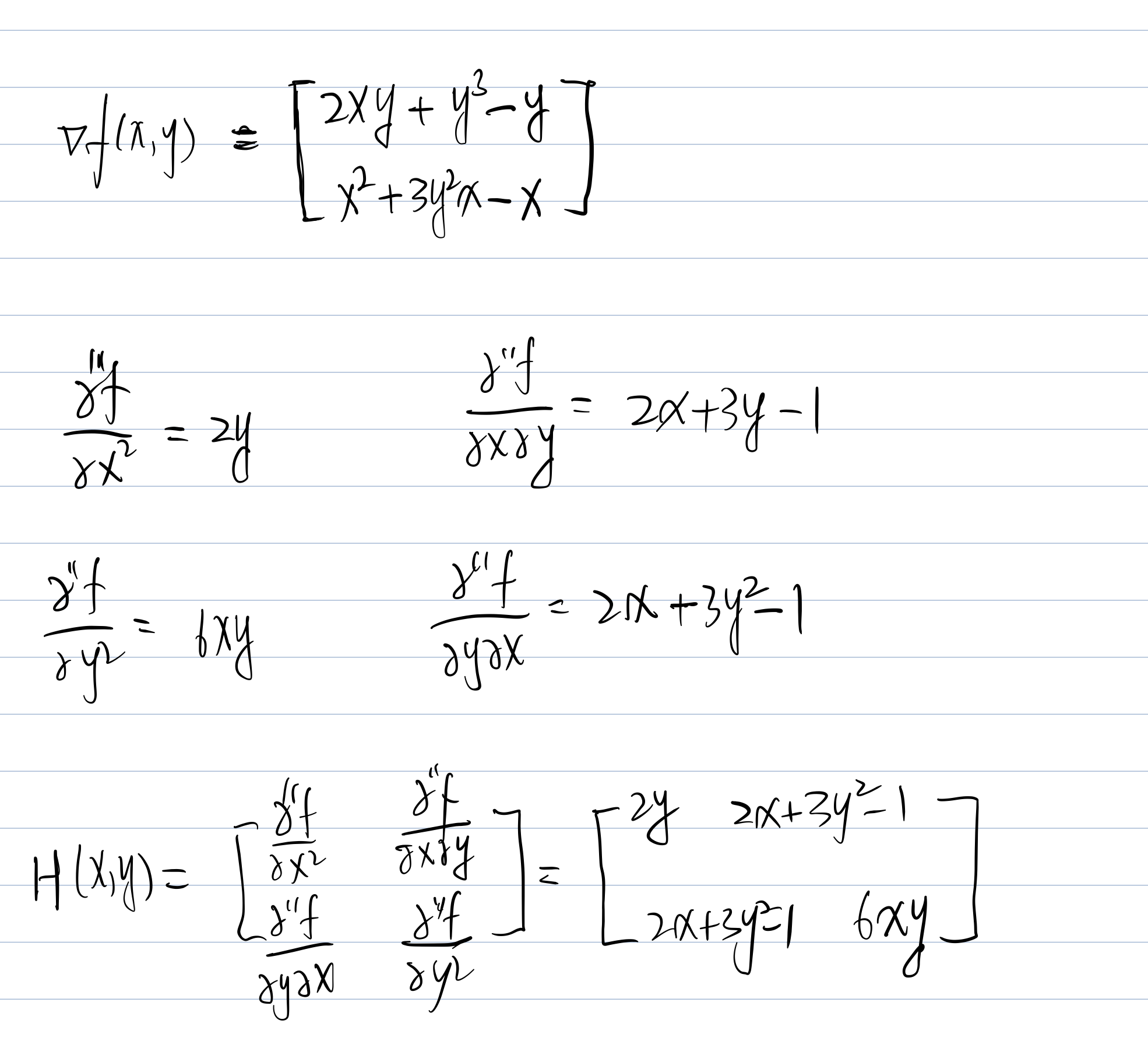
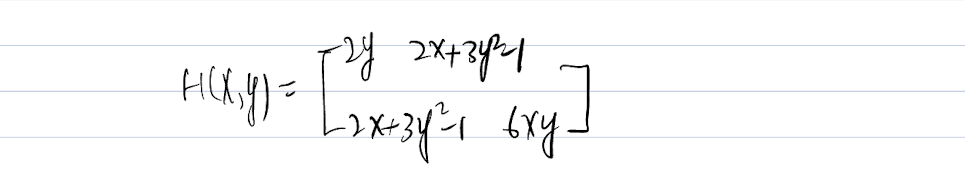
Then we need to check the $k$$k$the Leading principle minor to check the point is a local minimum or local maximum or not either of them.

Theorem:

If $LP{M}_k$$LPM_k$ > 0, then the H is positive definite, st.pt is local min.

If $(-1{)}^{k}LP{M}_k$$(-1)^k LPM_k$ > 0, then the H is negative definite, st.pt is local max.

 

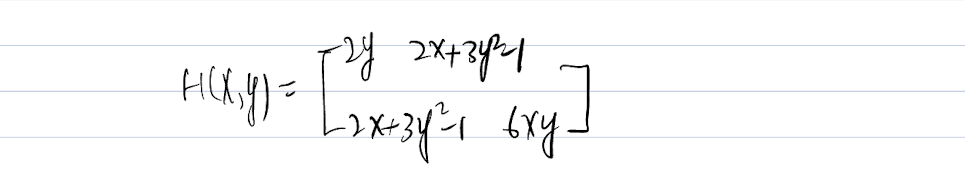
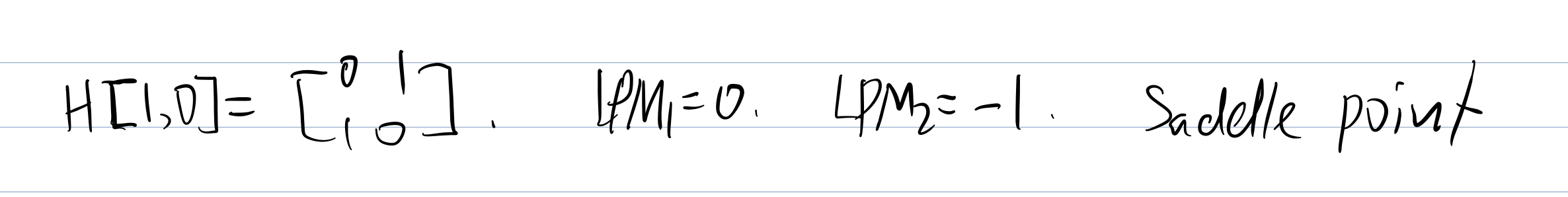
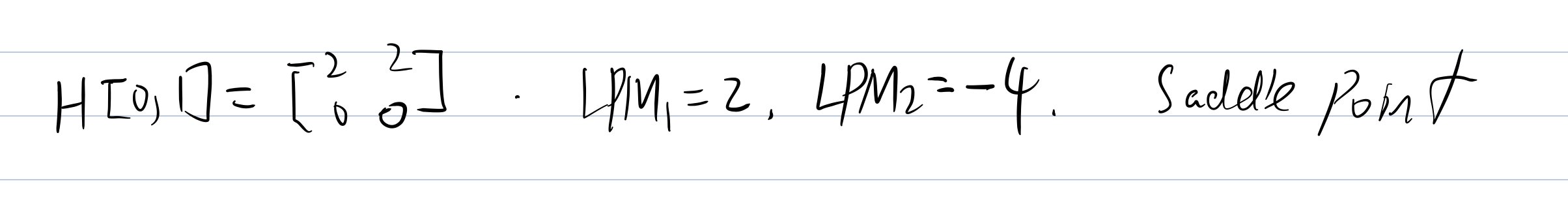
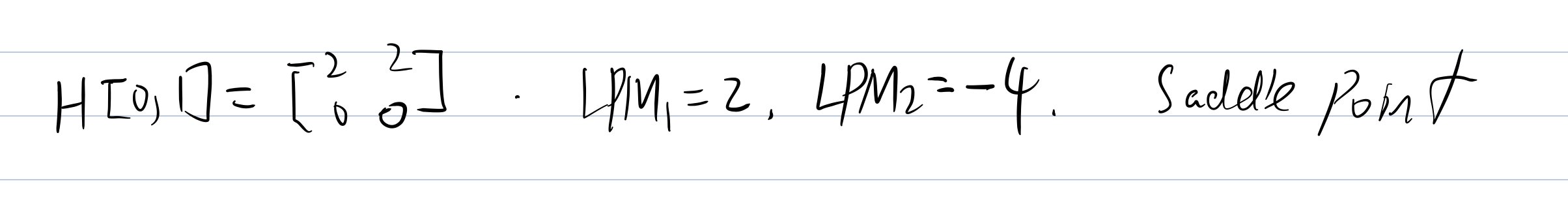
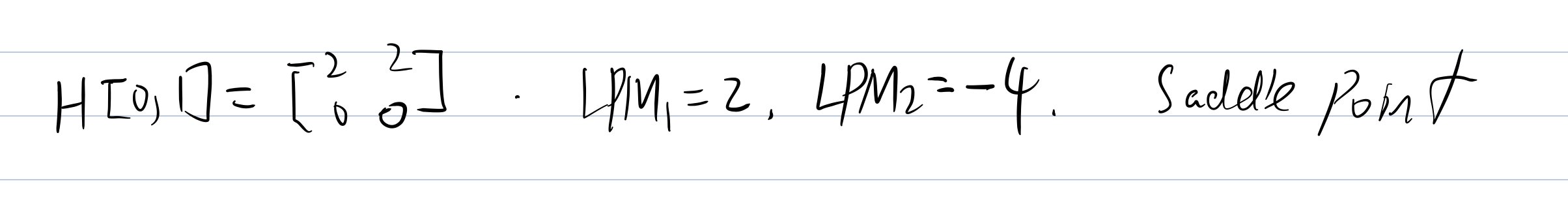
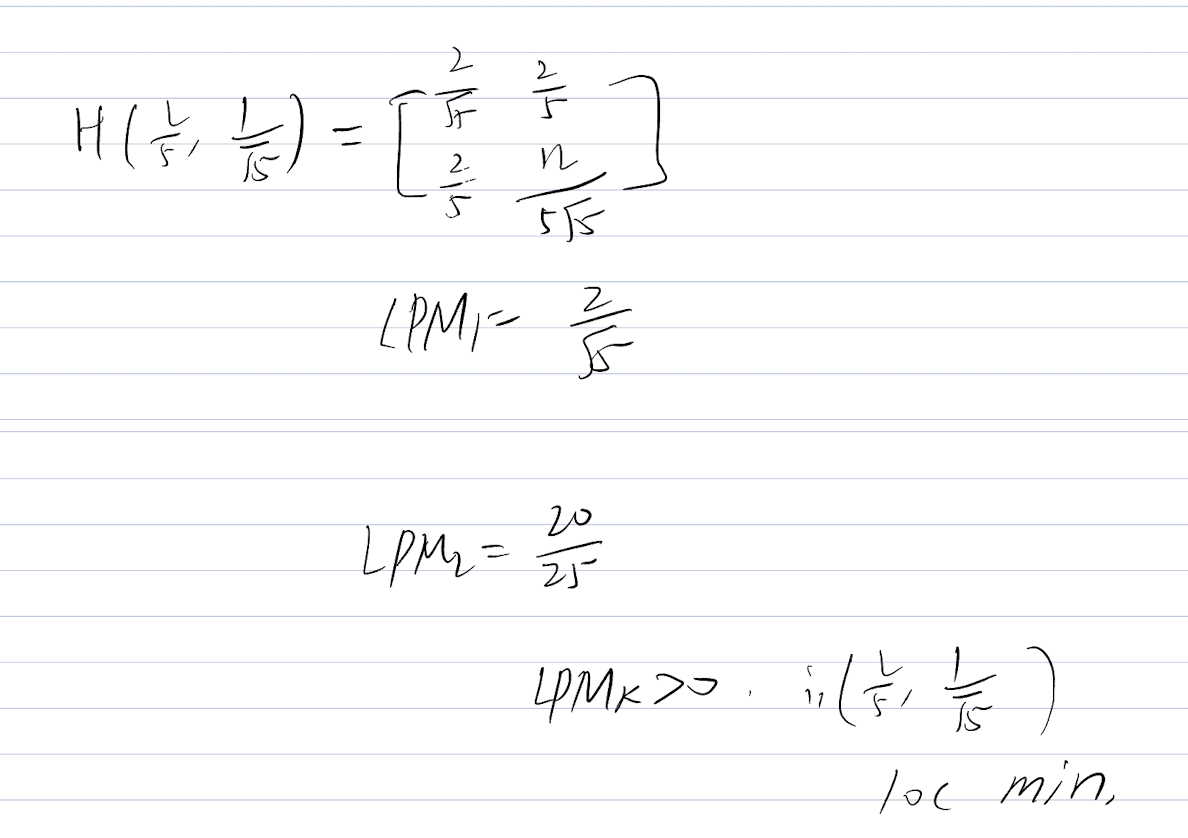
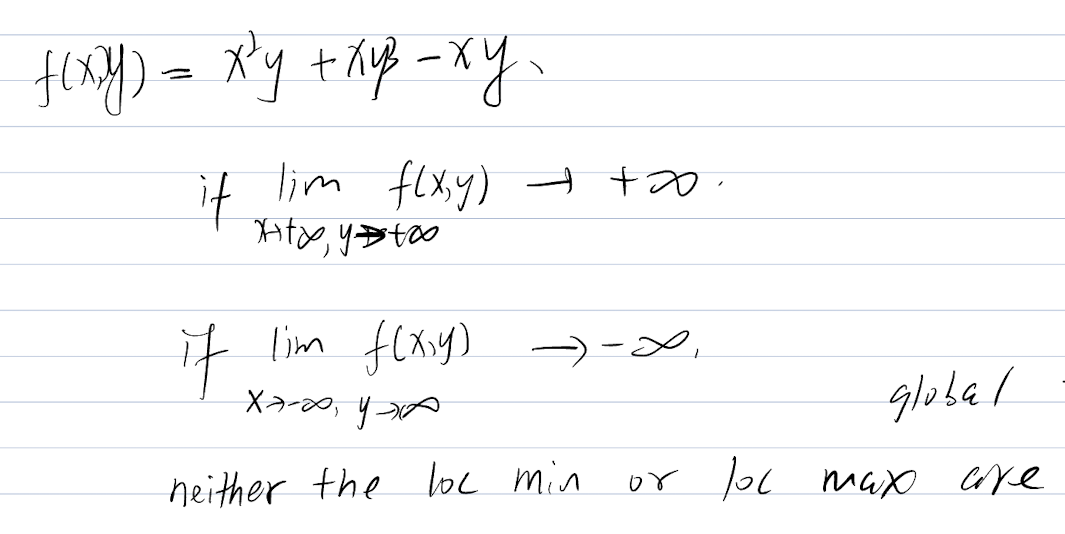
Unconstrained Optimization Done.

Extra

Quadratic Problems

QP is NLP where the largest power is Square (^2).

[End of 1214]

References