FE581 – 0522 - Logistic Regression and Clusstering Methods

4.3 Logistic Regression

library(ISLR2)
df <- Default
head(df)

  default student   balance    income
1      No      No  729.5265 44361.625
2      No     Yes  817.1804 12106.135
3      No      No 1073.5492 31767.139
4      No      No  529.2506 35704.494
5      No      No  785.6559 38463.496
6      No     Yes  919.5885  7491.559

str(df)

'data.frame': 10000 obs. of  4 variables:
 $ default: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
 $ student: Factor w/ 2 levels "No","Yes": 1 2 1 1 1 2 1 2 1 1 ...
 $ balance: num  730 817 1074 529 786 ...
 $ income : num  44362 12106 31767 35704 38463 ...

In the default data set

Rather than modeling this response Y directly, logistic regression models the probability that Y belongs to a particular category.

Because we want to estimate the probability of Y belongs to one of the particular category, that means the result of our estimation must fall into the range of [0,1]. but if we use normal linear regression, it wont able to achieve this. As in linear regression, the line can have any value even less than zero and bigger than one.

That is why we need logistic regression , where it can be written as:

$p(balance)$$p(balance)$ must have value between 0 and 1 (cause it is a probability).

4.3.1 The Logistic Model

Question: How should we model the relationship between $p(x)=Pr(Y=1|X)$$p(x)=Pr(Y=1|X)$ and $X$$X$ ?

If we use linear regression to represent this, then it will be:

$\begin{array}{}\text{(4.1)}& p(X)={\beta }_0+{\beta }_{1}X\end{array}$$\begin{align*} p(X) = \beta_0 + \beta_1X \tag{4.1} \end{align*}$ But it will introduce new problems, as we said earlier, the result of (4.1) can be negative, can be bigger than 1, so it dose not fit our target of predicting 'probability'. so we must find some other way to model it so that the result just sits between 0 and 1.

In logistic regression, the logistic function or the sigma function is used:

in our case, $f(x)={\beta }_0+{\beta }_{1}X$$f(x) = \beta_0 + \beta_1X$

So we can rewrite the logistic function as:

for Example:

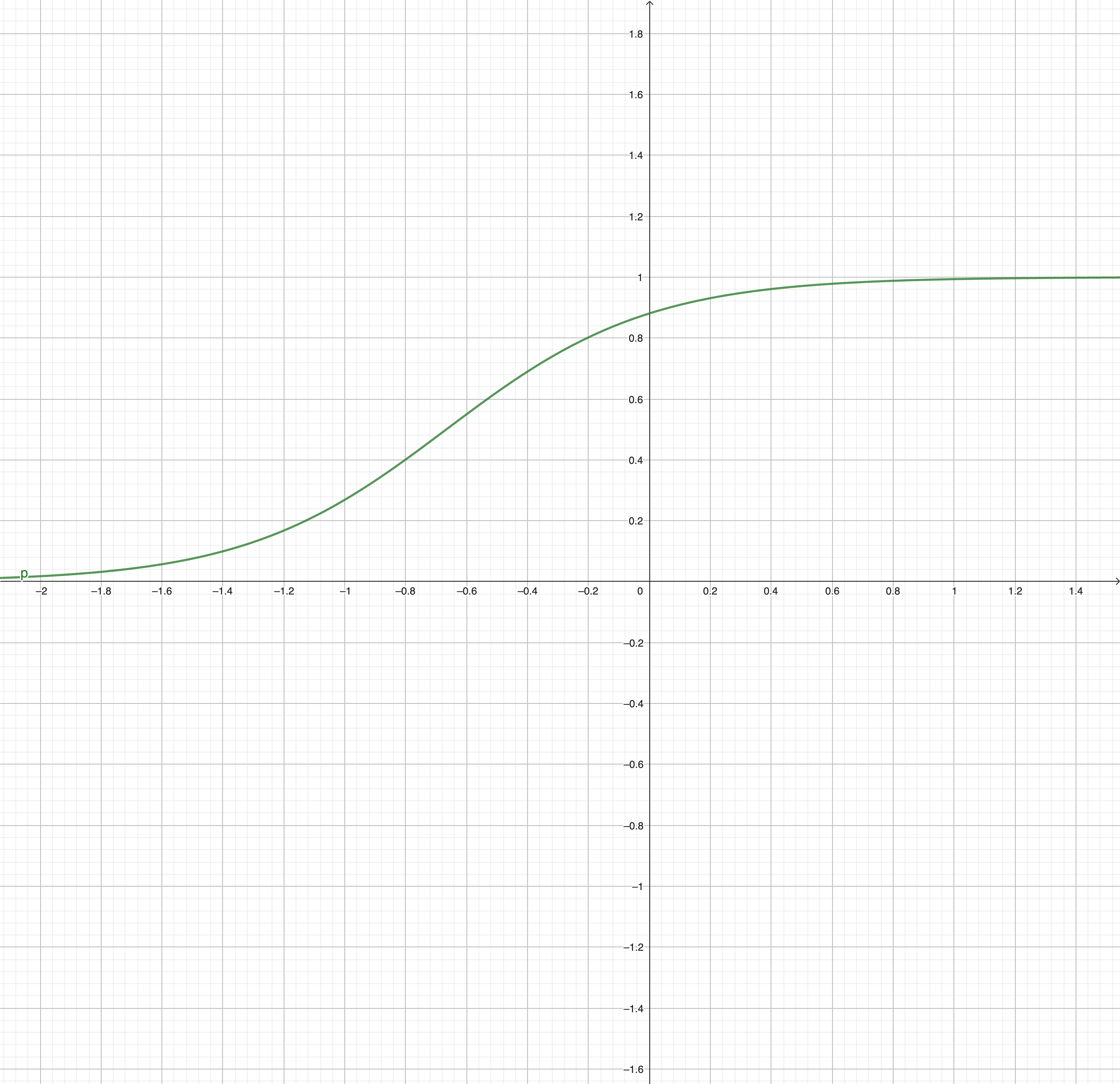
Then we can find that no matter what is the value of ${\beta }_0,{\beta }_1$$\beta_0,\beta_1$ and $x$$x$ is, the value of the function always lies between 0 and 1. (perfect for probability)

Now we have the function that satisfies our requirements for the output ( should be range between 0 and 1), our next job is to find the values of ${\beta }_0,{\beta }_1$$\beta_0, \beta_1$, it is obvious that we do not have the overall population data, so the values of ${\beta }_0,{\beta }_1$$\beta_0,\beta_1$ will always be unknown, so we use statistical estimations to find ${\hat{\beta }}_0,{\hat{\beta }}_1$$\hat \beta_0, \hat \beta_1$ which best estimates the values of ${\beta }_0,{\beta }_1$$\beta_0,\beta_1$.

We can rewrite the function in (4.2) in a slightly different way:

$\begin{array}{r}p(x)=\frac{e^{{\beta }_0+{\beta }_{1}X}}{1+e^{{\beta }_0+{\beta }_{1}X}}\\ \\ p(x)\cdot (1+e^{{\beta }_0+{\beta }_{1}X})=1+e^{{\beta }_0+{\beta }_{1}X}\\ \\ p(x)+p(x)\cdot e^{{\beta }_0+{\beta }_{1}X}=1+e^{{\beta }_0+{\beta }_{1}X}\\ \\ p(x)=1+e^{{\beta }_0+{\beta }_{1}X}-p(x)\cdot e^{{\beta }_0+{\beta }_{1}X}\\ \\ p(x)=(1-p(x))\cdot e^{{\beta }_0+{\beta }_{1}X}\\ \\ \frac{p(x)}{1-p(x)}=e^{{\beta }_0+{\beta }_{1}X}\end{array}$$\begin{split} p(x) = \frac{e^{\beta_0 + \beta_1X }}{1+e^{\beta_0 + \beta_1X}} \\\\ p(x)\cdot(1+e^{\beta_0 + \beta_1X}) = 1+e^{\beta_0 + \beta_1X} \\\\ p(x) + p(x)\cdot e^{\beta_0 + \beta_1X} = 1+e^{\beta_0 + \beta_1X} \\\\ p(x) = 1+e^{\beta_0 + \beta_1X} - p(x)\cdot e^{\beta_0 + \beta_1X} \\\\ p(x) = \big(1-p(x)\big)\cdot e^{\beta_0 + \beta_1X} \\\\ \frac{p(x)}{1-p(x)} = e^{\beta_0 + \beta_1X} \end{split}$

so we can achieve:

where the LHS: $\frac{p(x)}{1-p(x)}$$\frac{p(x)}{1-p(x)}$ is called the odds, and can take values between $(0,\mathrm{\infty })$$(0,\infty)$.

Odds basically means success ratio, such as one success out of five means we have $\frac{1}{5}=0.2$$\frac{1}{5}=0.2$ and it corresponds to odds=1/4. (1 success 4 failure)

By taking logarithm on (4.3) we can further make changes as:

the LHS is called as logit or log-odds, and we can easily realize that, the relationship between X and p(X) are not linear.

4.3.2 Estimating the regression Coefficients

As we talked earlier, we need to find ${\hat{\beta }}_0$$\hat \beta_0$ and ${\hat{\beta }}_1$$\hat \beta_1$ such that they are the closest (or best) estimaters of the ${\beta }_0$$\beta_0$ and ${\beta }_1$$\beta_1$

The process of finding ${\hat{\beta }}_0$$\hat \beta_0$ and ${\hat{\beta }}_1$$\hat \beta_1$ evolves a statistical method named as "maximum likelihood" and given by the Maximum Likelihood Function :

From the formula we can say the actually what maximum likelihood dose is it is trying to maximize the probability of binomial success outcome.

By using some programming languages like R or Python or maybe Excel (lol it is not a programming language) we can get the estimated values of the (4.3) or (4.2), which are the coefficients of the logistic function.

And statistically we will get the resulting table:

$\begin{array}{r}f(X)=e^{{\beta }_0+{\beta }_1{x}_1}=e^{-10.65+0.0055x_1}\\ p(X)=\frac{e^{f(X)}}{1+e^{f(X)}}=\frac{e^{-10.65+0.0055x_1}}{1+e^{-10.65+0.0055x_1}}\end{array}$$\begin{split} f(X) = e^{\beta_0+\beta_1 x_1} = e^{-10.65 + 0.0055 x_1} \\ p(X) = \frac{e^{f(X)}}{1+e^{f(X)}} = \frac{e^{-10.65 + 0.0055 x_1}}{1+e^{-10.65 + 0.0055 x_1}} \end{split}$ or we can also get the function for odds:

4.3.3 Making Predictions

It is as easy as putting the values back into our function. if x is a quantitative variable (numerical) we just simply put x back into the formula of (4.2) or (4.3). If x is a qualitative variable (categorical) we use dummy variable that takes the value of 1 or 0, then put it back to the formula.

4.4.4 multiple logistic regression

In multiple x case, the formula for slightly changes into: $\begin{array}{rl}f(X)& ={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p\\ \\ p(X)& =\frac{e^{{\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p}}{1+e^{{\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p}}\\ \\ \frac{p(X)}{1-p(X)}& =e^{{\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p}\\ \\ ln(\frac{p(X)}{1-p(X)})& ={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p\end{array}$$\begin{split} f(X) &= \beta_0 + \beta_1x_1 +...+ \beta_p x_p \\\\ p(X) &= \frac{e^{\beta_0 + \beta_1x_1 +...+ \beta_p x_p}}{1+e^{\beta_0 + \beta_1x_1 +...+ \beta_p x_p}} \\\\ \frac{p(X)}{1-p(X)} &= e^{\beta_0 + \beta_1x_1 +...+ \beta_p x_p} \\\\ ln(\frac{p(X)}{1-p(X)} )&= \beta_0 + \beta_1x_1 +...+ \beta_p x_p \end{split}$

10.3 Clustering Methods

Clustering is an unsupervised learning method, which aims to find relationships between either:

1. observations on the different row (grouping)

2. variables on the different column (reasoning)

Simply, it is a method to put similar things together.

So one of the most important things to consider in clustering methods is how we define things (observations) are similar

10.3.1 K-Means Clustering

Algorithm:

We have n data observations as $x_1(,,..,),x_2(,,..,),...x_n(,,..,)$$x_1(,,..,),x_2(,,..,),...x_n(,,..,)$.

1. Randomly assign each observation point to a cluster $K_i$$K_i$, (or can be written as to a cluster center $C_i$$C_i$)

2. Compute the centroid (mean) of each cluster ${\mu }_1,{\mu }_2,...,{\mu }_K$$\mu_1,\mu_2,...,\mu_K$

3. Calculate the Euclidian distance between each class centroid ${\mu }_i$$\mu_i$ and each observation point $x_i$$x_i$ , as $d(x_i,{\mu }_i)$$d(x_i,\mu_i)$

4. Reassign the observation $x_j$$x_j$ to the cluster $K_j$$K_j$ which has the minimum distance $d(x_j,{\mu }_j)$$d(x_j,\mu_j)$

5. repeat 1-4 until we get a minimal total within class variation(mean of Euclidian distances) or SSE (Sum of Squared Error ,calculated as total Euclidian distances).

Calculation Example:

10.3.2 Hierarchical Clustering

One potential disadvantages of K-means is that we need to first define the # of clusters.

Main tasks in hierarchical clustering includes:

1. How to draw the dendrogram

2. How to cut the dendrogram (where to cut)

3. How to evaluate the model

To build a dendrogram (bottom to top approach):

1. Calculate the dissimilarities between each observations. (to build up from the bottom)

   1. Manhattan Distance ($|x_1-x_2|+|y_1-y_2|$$|x_1-x_2|+|y_1-y_2|$)

   2. Euclidian Distance Squared ($d^2=(x_1-x_2{)}^2+(y_1-y_2{)}^2$$d^2 =(x_1-x_2)^2+(y_1-y_2)^2$)

   3. Euclidian Distance ($d^2=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$d^2 =\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$)

2. Pick the minimum distance and fuse.

3. Calculate the linkage between groups of observations. (to build up further branches)

   1. complete

   2. average

   3. single

   4. centroid

4. Pick the minimum linkage and fuse.

5. repeat 1-4 until we reach the root of the dendrogram.

When calculating the linkage, there are 4 different methods as given above, and we have different calculation approach, let's assume in some time, we end up with two cluster sets as $x_1,x_2$${x_1,x_2}$ and $x_4,x_5$${x_4,x_5}$

1. Single Linkage: Find the minimum distance between any point in the first set to any point in the second set. That is, find the minimum among the distances d(x1,x4), d(x1,x5), d(x2,x4), and d(x2,x5). This minimum distance is the single linkage distance.

2. Complete Linkage: Find the maximum distance between any point in the first set to any point in the second set. That is, find the maximum among the distances d(x1,x4), d(x1,x5), d(x2,x4), and d(x2,x5). This maximum distance is the complete linkage distance.

3. Average Linkage: Calculate the average of all the distances between points in the first set to points in the second set. That is, calculate the average of the distances d(x1,x4), d(x1,x5), d(x2,x4), and d(x2,x5). This average distance is the average linkage distance.

4. Centroid Linkage: Calculate the centroids of the two sets first. The centroid of a set is the point whose coordinates are the average of the coordinates of all the points in the set. Let c1 be the centroid of {x1,x2} and c2 be the centroid of {x4,x5}. Then, calculate the distance between these two centroids, d(c1,c2). This distance is the centroid linkage distance.